Stefan Hoch

Frank Reinhold

Bernhard Werner

Kristina Reiss

Jürgen Richter-Gebert

Supported by the Heinz Nixdorf Foundation

Fractions

Introduction

Fractions. Getting in touch with rational numbers
1st Edition

Stefan Hoch,
Frank Reinhold,
Bernhard Werner,
Kristina Reiss,
Jürgen Richter-Gebert

Technical University of Munich, 2018.

Supported by the Heinz Nixdorf Foundation

Translation: Saskia Brose, Erin Kim, Frank Reinhold, Stefan Hoch

License:
This work is licensed under a Creative Commons Attribution–NonCommercial–NoDerivatives 4.0 International License.

Citation:
Hoch, S., Reinhold, F., Werner, B., Reiss, K., Richter-Gebert, J. (2018). Bruchrechnen. Bruchzahlen & Bruchteile greifen & begreifen [Web Version] (4. Aufl.). München, Technische Universität München.

Technical University of Munich
TUM School of Education
Heinz Nixdorf-Chair of Mathematics Education

Arcisstraße 21
80333 Munich

www.ma.edu.tum.de

Preface

Alice was beginning to get very tired of sitting by her sister on the bank, and of having nothing to do: once or twice she had peeped into the book her sister was reading, but it had no pictures or conversations in it, »and what is the use of a book,« thought Alice »without pictures or conversation?«

This is the very beginning of Lewis Carroll’s famous book Alice in Wonderland.

Our book about fractions does not necessarily have a lot of conversation, but rather a lot of pictures – interactive pictures, to be exact. While creating this iBook, we sought to capture the somewhat unintuitive topic of fractions: ... “Is [~] now greater than or less than [~]?“– by using pictures and animations in an interactive way. Our book of fractions is an interactive workbook, and there is a lot to do. Problems – and of course games – can be directly worked on or played with using an iPad. The solution fields can simply be filled in with the touch of a finger, as long as the writing is legible.

This has made this small booklet an experiment in two ways. It is a didactical experiment, but also a technological experiment. We truly believe that in this respect, we have written a very special iBook: one which is interactive, with built-in learning aids, games, exercises, visualizations, and memory games.

We hope that the readers of this book enjoy this iBook as much as we have enjoyed writing it.

Munich, March 2018
Jürgen Richter-Gebert

Instructions

In these boxes you can write your answer directly with your finger. Do your best to write as neatly as possible!
Tap here to check your answers. You will see similar buttons depending on the type of exercise.
Tap here to exit the exercise.
Tap here to get additional information for the exercise or to reset the level of difficulty.
Tap here to get a hint. The higher the light on the traffic light, the more the tip will tell you.

Here is an example of a problem. All of the problems in this book will look similar to this.

Tap the blue arrow!

Resetting all problems

Your progress will be saved as you work through this book. You can also reset all of the problems if you want to reset your progress and start over from the beginning. To do this, tap on the arrow on the right and follow the instructions.

Getting in touch with rational numbers

Dividing a pizza

Anna wants to share a pizza with five of her friends. She cuts the pizza into six pieces. All of the pieces are of equal size.

Which statements are true?

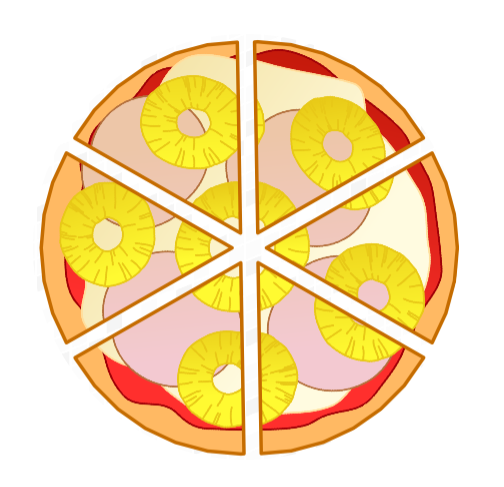
Here is the pizza again.

Can you explain how Anna cut the pizza? Write down your answer and then compare it with a neighbor.

Writing fractions

A pizza is divided into eight equal pieces. Mia takes three of these pieces.

You can call this: "Three Eighths", and write:

The new notation $\frac38$ consists of two numbers which each have different meanings:

"The eight tells us how many equal parts the pizza is divided into. The three tells us how many of these parts are taken."

A chocolate bar has twelve pieces. Tom takes seven pieces.

Fill in the blanks.

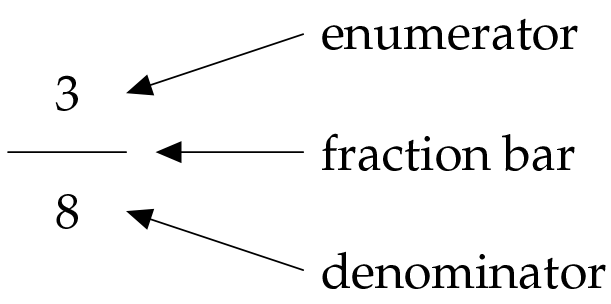
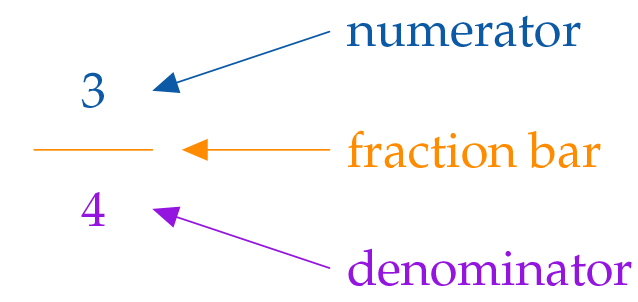
Compare your answer with a neighbor. Then discuss similar problems with round pizzas and rectangular chocolate bars. Can you make your own fractions with pizzas and chocolate bars?

Parts of a whole can be written as fractions:

The denominator tells us how many equal parts the whole is divided into.

The numerator tells us how many of these parts are being considered.

Numerator and denominator are separated by the fraction bar.

You can say: "three fourths", and write:

One more tip

The denominator can be less than, equal to, or even greater than the numerator. For example:

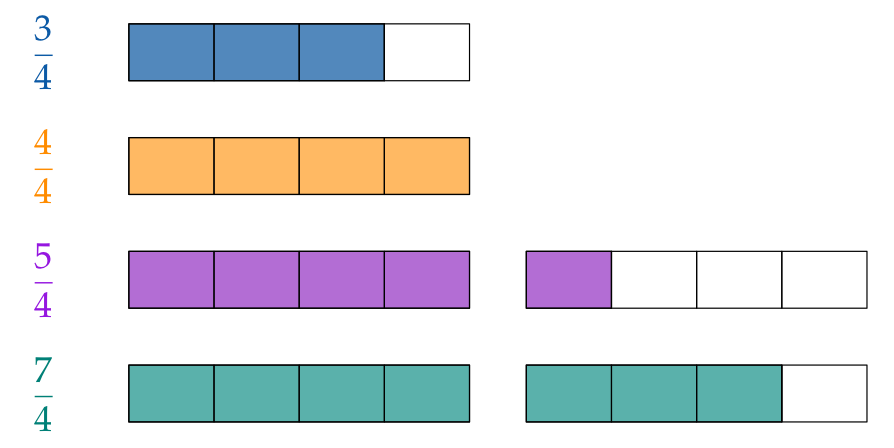
When the numerator is greater than the denominator, that means the fraction represents more than a whole.

There is one pair of equivalent fractions hidden in the cards below. Who can match more pairs?

Calculating a part of something

Filling up a pitcher

A pitcher can hold one liter of water. Try experimenting with the amount of water in the pitcher. You can also read off the fractions labeled on the pitcher based on the amount of water in the pitcher.

Fill the pitcher with water and determine the correct fraction. Look at the calculation step by step.

Splitting a distance

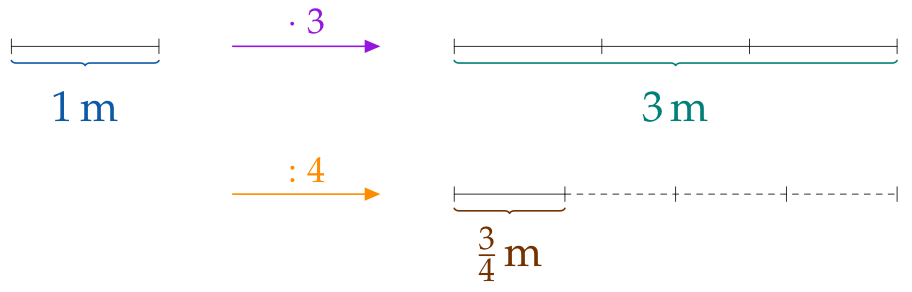
You can get a $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\textrm{m}$ long distance by…

  1. taking a $1\,\text{m}$ long distance and dividing it into four equal parts and then...

  2. taking 3 of these parts:

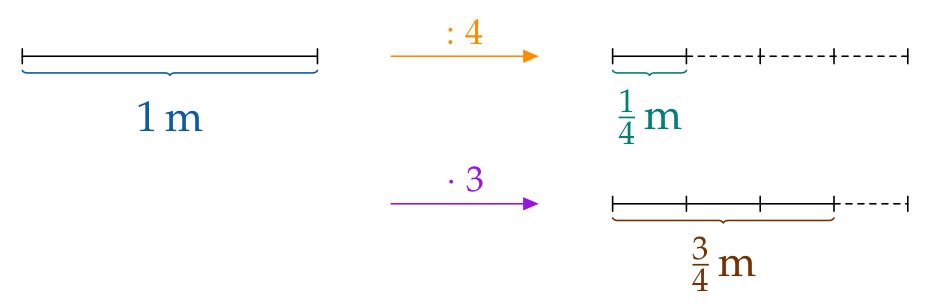
$\frac34\,\text{m}$ are 3 fourths of a (whole) meter.

And without the diagram above...?

Solve the next exercise without using a diagram.

Determine $\frac57$ of a $21\,\text{m}$ long distance. You can proceed in two steps:

This is how you can easily calculate a part of a whole:

$$\frac{{\color{#9516E0}5}}{{\color{#FF8C00}7}}\text{ of }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#FF8C00}\,:\,}{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$

Need more help?

You can get hints for some of the problems. Tap the little traffic light in the top right corner of the exercise for help.

What about the other way around ...?

If $\frac13$ of a lesson is $15\,\text{min}$, how long is the whole lesson?

$$15\,\text{min}\cdot \color{#0C5AA6}{3} = 45\,\text{min}$$

Fractions with a numerator of 1 (e. g. $\frac13, \frac12$ or $\frac17$) are called unit fractions.

As you can see, the original value can easily be calculated if the fraction is a unit fraction.

Using distances once more, we will now show you how to proceed if the fraction is not a unit fraction.

Creating a whole meter

f you start with a $\frac34\,\text{m}$ long distance, you can get the full length of one meter…

  1. Divide the distance into three equal parts and then…
  2. Add together four of those equal parts:

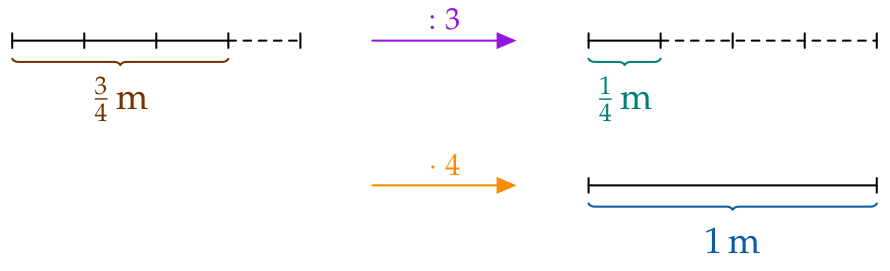
$\frac34\,\text{m}$ are 3 fourths of a (whole) meter.

If $\frac{\color{#9516E0}5}{\color{#FF8C00}7}$ of a distance are $15\,\text{m}$, how long is the whole distance?

If the fraction "$\frac{\color{#9516E0}5}{\color{#FF8C00}7}$" and the fractional amount "$15\,\text{m}$" are given, the whole can be determined. You can apply this method the other way around as well:

$$\Big({{15\,\text{m}}}~{\color{#9516E0}{:5}}\Big){\color{#FF8C00}\cdot}{\color{#FF8C00}7}= 3\,\text{m}{\color{#FF8C00}\cdot}{\color{#FF8C00}7}= {{21\,\text{m}}}$$

Sharing pizza and chocolate

Donatello the pizza baker is having problems in the kitchen

On top of that, his four guests want to share their pizzas.

Help Donatello to evenly split the three pizzas among the four guests.

Recap

Since the pizzas are supposed to be shared equally, each guest will receive the same amount.

At the end, each guest will have $\frac14$ of three pizzas. This is the same as $\frac34$ of one pizza.

Three chocolate bars are shared by four children

Tim, Carl, Will and Gaby are looking forward to their chocolate bars.

How much chocolate does each child get?
Which answers are true?

A different way of splitting a distance

You can also get the fraction $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\text{m}$ by:

  1. Dividing a $3\,\text{m}$ long distance into 4 equal parts and…
  2. taking 1 of those parts.

$\frac34\,\text{m}$ is the same as $\frac14$ of three (whole) meters.

And without the diagram above ...?

Solve the next exercise without a drawing.

Complete the text.

There are two different ways to calculate $\frac{\color{#9516E0}5}{\color{#FF8C00}7}$ of $21\,\text{m}$:

$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ of }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#9516E0}\cdot}{\color{#9516E0}5}\Big)~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= 105\,{\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= {15\,{\text{m}}}$$

or

$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ of }{{21\,\text{m}}}= \Big({21\,\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$

As you can see you get the same results – both calculations are correct

Paul’s math homework

Paul is in fourth grade and is doing his math homework. He lets his older brother Max, who is in sixth grade, check it:

Dividing arbitrary numbers

So far you have not been able to solve division problems where the divisor is greater than the dividend. Your solution would always have a remainder:

$$\begin{aligned}3:11 &= 0\ \text{R}\ 3\\ 5:6& = 0\ \text{R}\ 5\end{aligned}$$

With fractions you can avoid having a remainder. The calculation ${\color{#0C5AA6}3}:\color{#FF8C00}{11}$ can be understood as:

"Divide 3 wholes into 11 equal parts."

The result is the fraction $\frac{\color{#0C5AA6}{3}}{\color{#FF8C00}{11}}$, so: $$\begin{aligned}3:11 &= \frac{3}{11}\\[1em] 5:6& = \frac56\end{aligned}$$

You can divide any natural number by another, regardless of whether your result would have a remainder. The result can now always be written as a fraction.

The fraction $\frac{{\color{#0C5AA6}3}}{{\color{#FF8C00}4}}$ is another way to write the quotient ${\color{#0C5AA6}3}:{\color{#FF8C00}4}$

With the help of fractions you can divide all natural numbers by each other, for example:

$3:4=\frac34,\quad 5:2=\frac52,\quad 3:7=\frac37,\quad 5:6=\frac56$

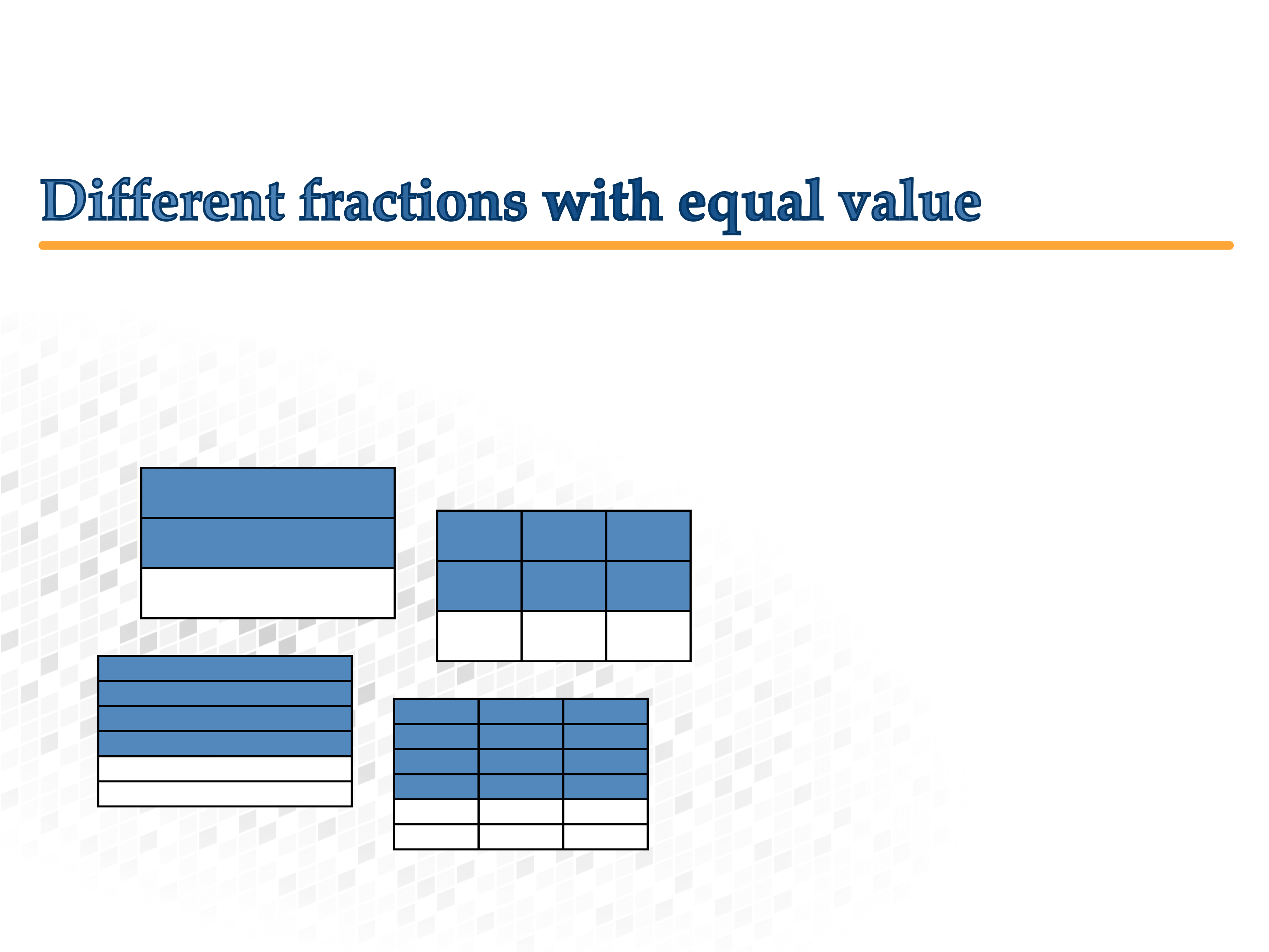
Different fractions with equal value

Folding a piece of paper

Cut out a square from a piece of paper. Color in one half of the square.

Fold the paper and discuss with a neighbor what you would call the fraction now. Write down your observations.
Dividing a square.

Equivalent fractions

With the help of the widget try to find fractions that look different, but are actually equal in value.

Use the adjustments below to find different fractions that have the same value.

And now without the diagram…

Marie says: "I noticed that I always have to do the same to the top and the bottom of the fraction!"

What does Marie mean by this?

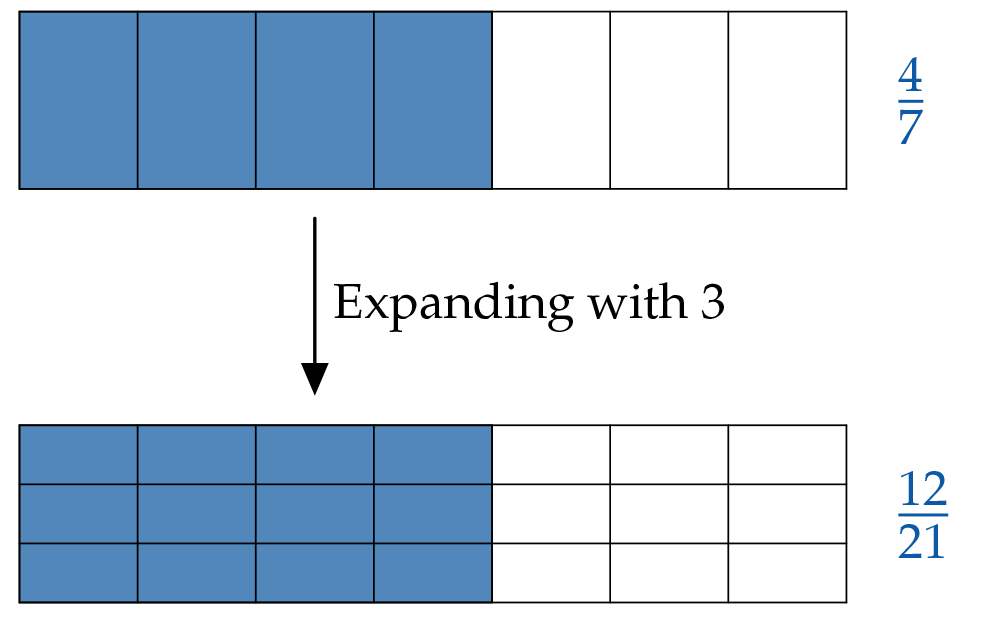
Write down a strategy, that helps you find equivalent fractions. Compare your answer with your neighbor.

Expanding is multiplying the numerator and denominator by the same number.

The number you expand the fraction by is written above the equal sign:

$$\frac47 \begin{matrix} \color{#0C5AA6}3\\ =\\ \phantom{3} \end{matrix} \frac{4{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}{7{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}=\frac{12}{21} $$

Expanding creates more divisions:

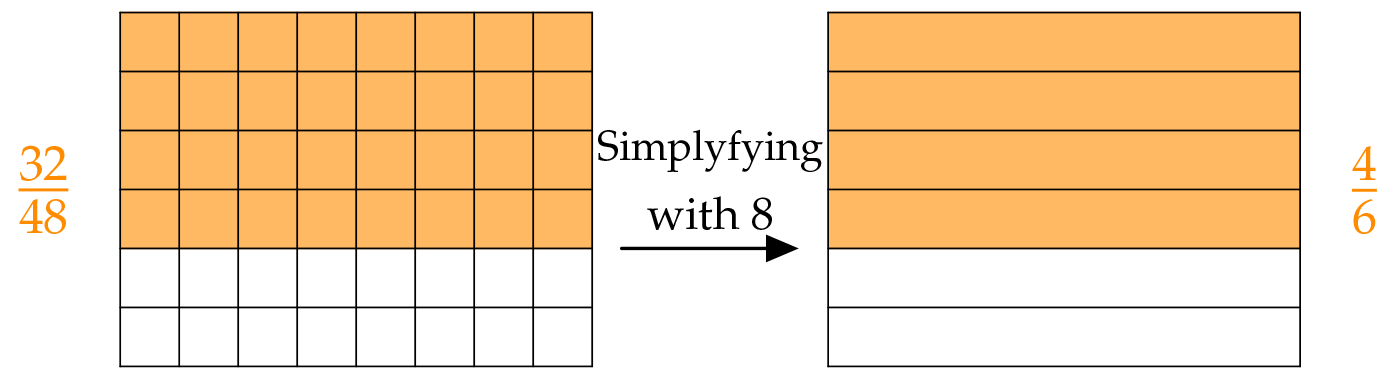
Simplifying is dividing the numerator and denominator by the same number.

The number you simplify the fraction by is written beneath the equal sign:

$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#FF8C00}8 \end{matrix} \frac{32{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}{48{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}= \frac{4}{6} $$

Simplifying creates less divisions:

Continuing to simplify

You can simplify fractions that have common factors in the numerator and denominator.

Consider the fraction $\frac{32}{48}$. The common factors of the numerator "32" and denominator "48" are 8, 2 and 18. This means that there are several different ways to simplify the fraction $\frac{32}{48}$:

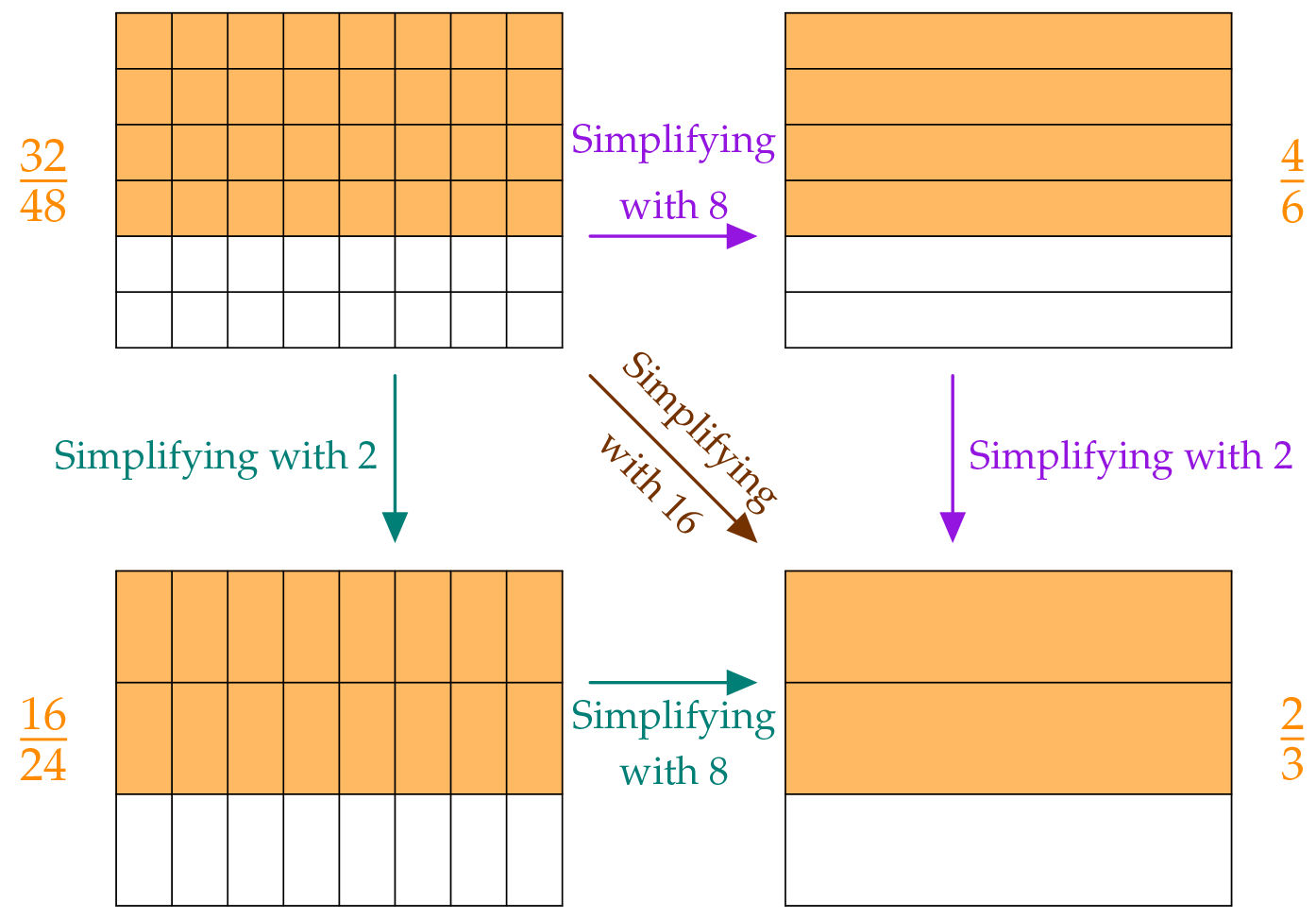
And now without the picture…

Our steps can also be written down in the following calculations:

$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#9516E0}8 \end{matrix} \frac{32{\,\color{#9516E0}:\,}{\color{#9516E0}8}}{48{\,\color{#9516E0}:\,}{\color{#9516E0}8}}= \frac{4}{6} \begin{matrix} \phantom{2}\\ =\\ \color{#9516E0}2 \end{matrix} \frac{4{\,\color{#9516E0}:\,}{\color{#9516E0}2}}{6{\,\color{#9516E0}:\,}{\color{#9516E0}2}}= \frac23 $$

or

$$ \frac{32}{48} \begin{matrix} \phantom{2}\\ =\\ \color{#008077}2 \end{matrix} \frac{32{\,\color{#008077}:\,}{\color{#008077}2}}{48{\,\color{#008077}:\,}{\color{#008077}2}}= \frac{16}{24} \begin{matrix} \phantom{8}\\ =\\ \color{#008077}8 \end{matrix} \frac{16{\,\color{#008077}:\,}{\color{#008077}8}}{24{\,\color{#008077}:\,}{\color{#008077}8}}= \frac23 $$

or

$$ \frac{32}{48} \begin{matrix} \phantom{16}\\ =\\ \color{#753200}{16} \end{matrix} \frac{32{\,\color{#753200}:\,}{\color{#753200}{16}}}{48{\,\color{#753200}:\,}{\color{#753200}{16}}}= \frac23 $$

The numerator and denominator of the fraction $\frac23$ do not have any common factors. This means that this fraction is completely simplified.

Expanding and simplifying do not change the value of the fraction.

A fraction can only be simplified by the common factors of the numerator and denominator.

If the numerator and denominator do not have any common factors, the fraction is completely simplified.

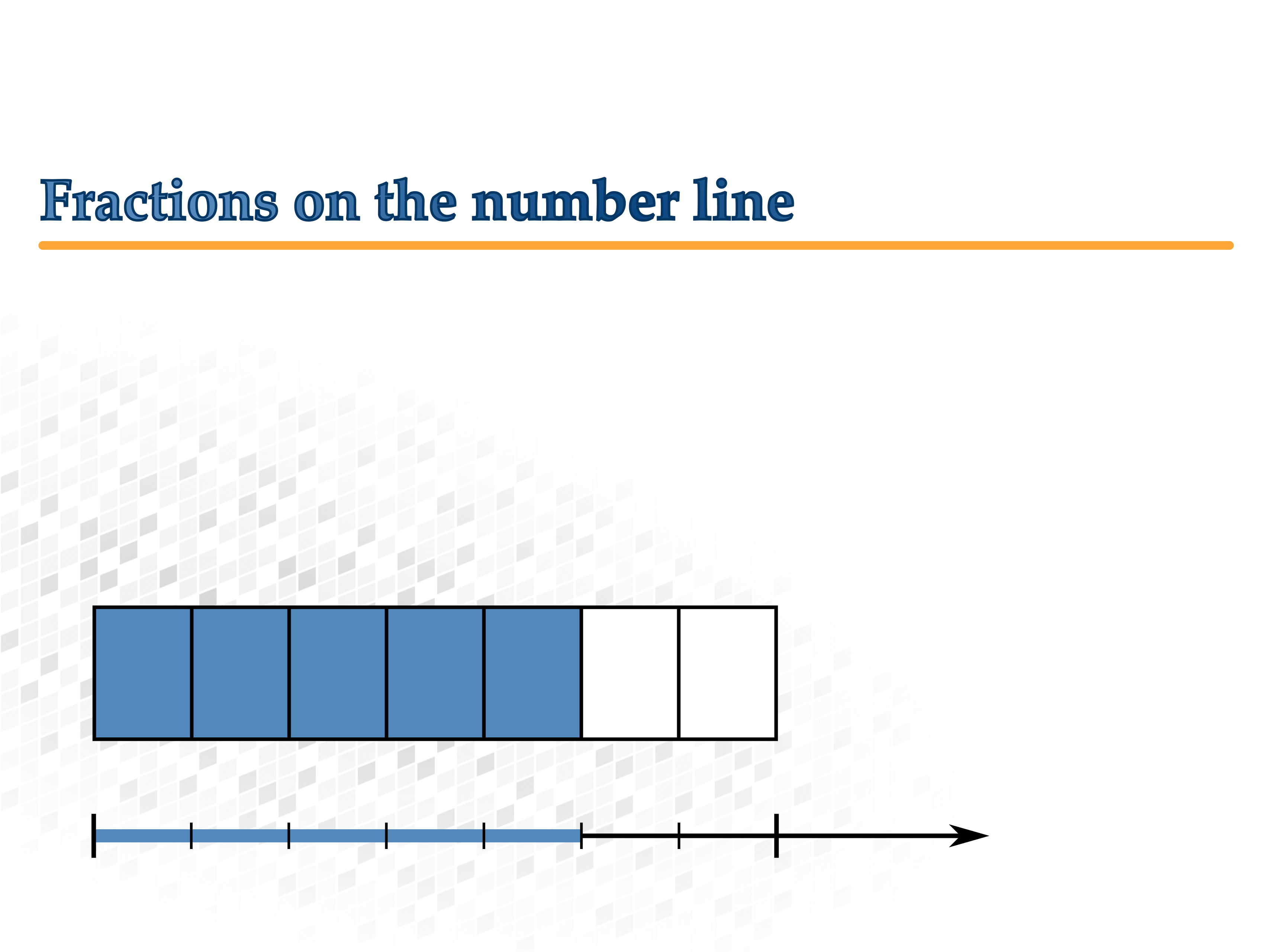
Fractions on the number line

Unwinding a circle

What do the fractions on the number line represent?

Watch the animation. Then, try experimenting with different denominators.

Shrinking a rectangle

Try picturing the number line as a "narrow rectangle".

Watch the animation of the rectangle and experiment with different denominators.

Fractions can be represented on the number line. You can picture the number line as an uncoiled circle:

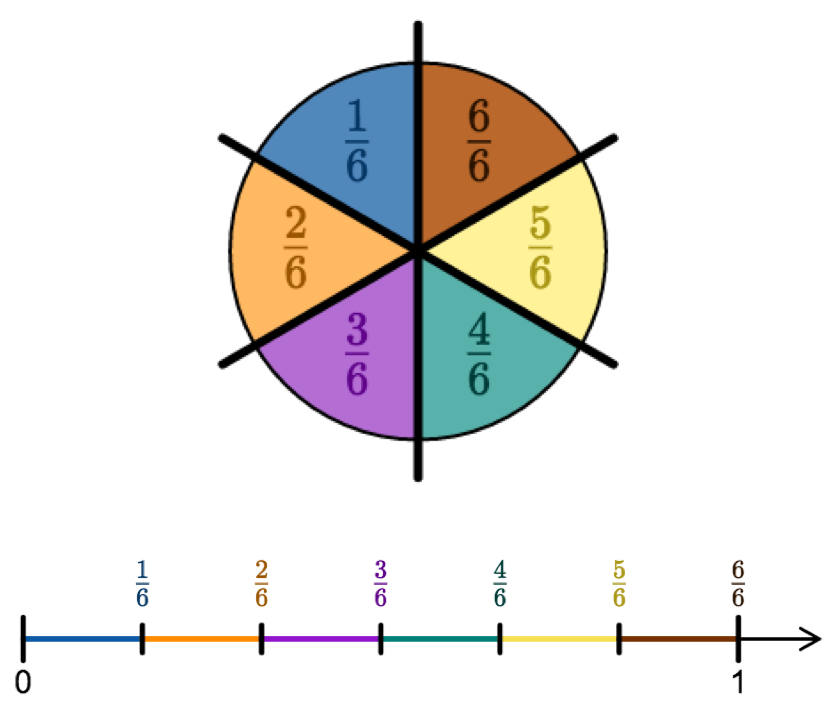
Fractions that are less than a whole are called proper fractions. They are between the 0 and the 1 on the number line. Their numerator is less than their denominator.

And to the right of the 1?

There is endless room to the right of the 1 on the number line. The fractions there are greater than a whole.

Watch the animation of the rectangle and experiment with different fractions.

Fractions can represent something that is greater than a whole. On the number line they look like this:

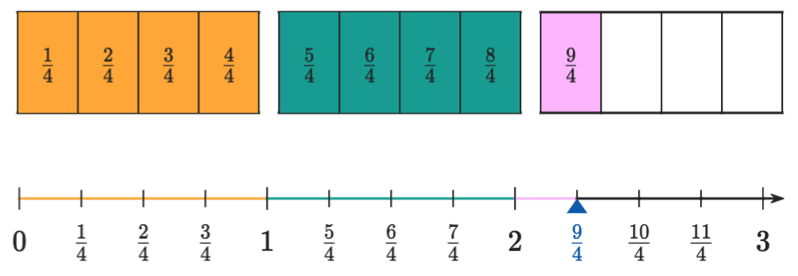
Fractions that are greater than a whole are called improper fractions. They are to the right of the 1 on the number line. Their numerator is greater than their denominator.

And in between?

Sometimes the divisions on the number line are not exact enough to represent fractions with large denominators. This means that you have to add more divisions.

Watch the animation of the rectangle and experiment with different fractions.

If the division is not exact enough, more divisions must be added:

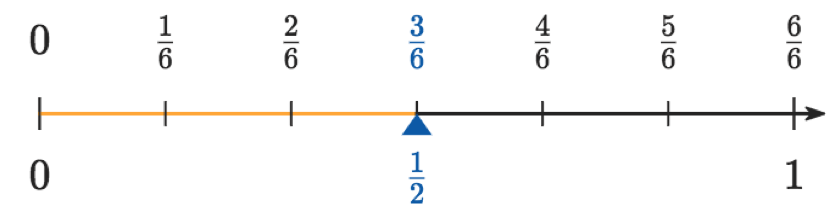
Spot already taken?!

Some fractions share the same spot on the number line:

In the last exercise you saw that the fractions $\frac13$ and $\frac26$ have the same position on the number line. This was also the case for the fractions $\frac{10}{6}$ and $\frac53$.

If you remember what you learned in the last chapter, you should understand why these fractions occupy the same position:

$$ \frac13 \begin{matrix} 2\\ =\\ \phantom{2} \end{matrix} \frac26 \quad \text{ and } \quad \frac{10}6 \begin{matrix} \phantom{2}\\ =\\ 2 \end{matrix} \frac{5}{3} $$

The fractions have the same value, because you can get one fraction by expanding or simplifying the other.

Every fraction can be positioned on the number line. Equivalent fractions share the exact same position on the number line!

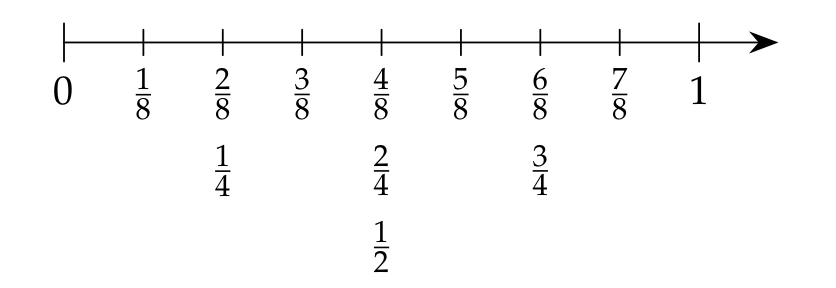
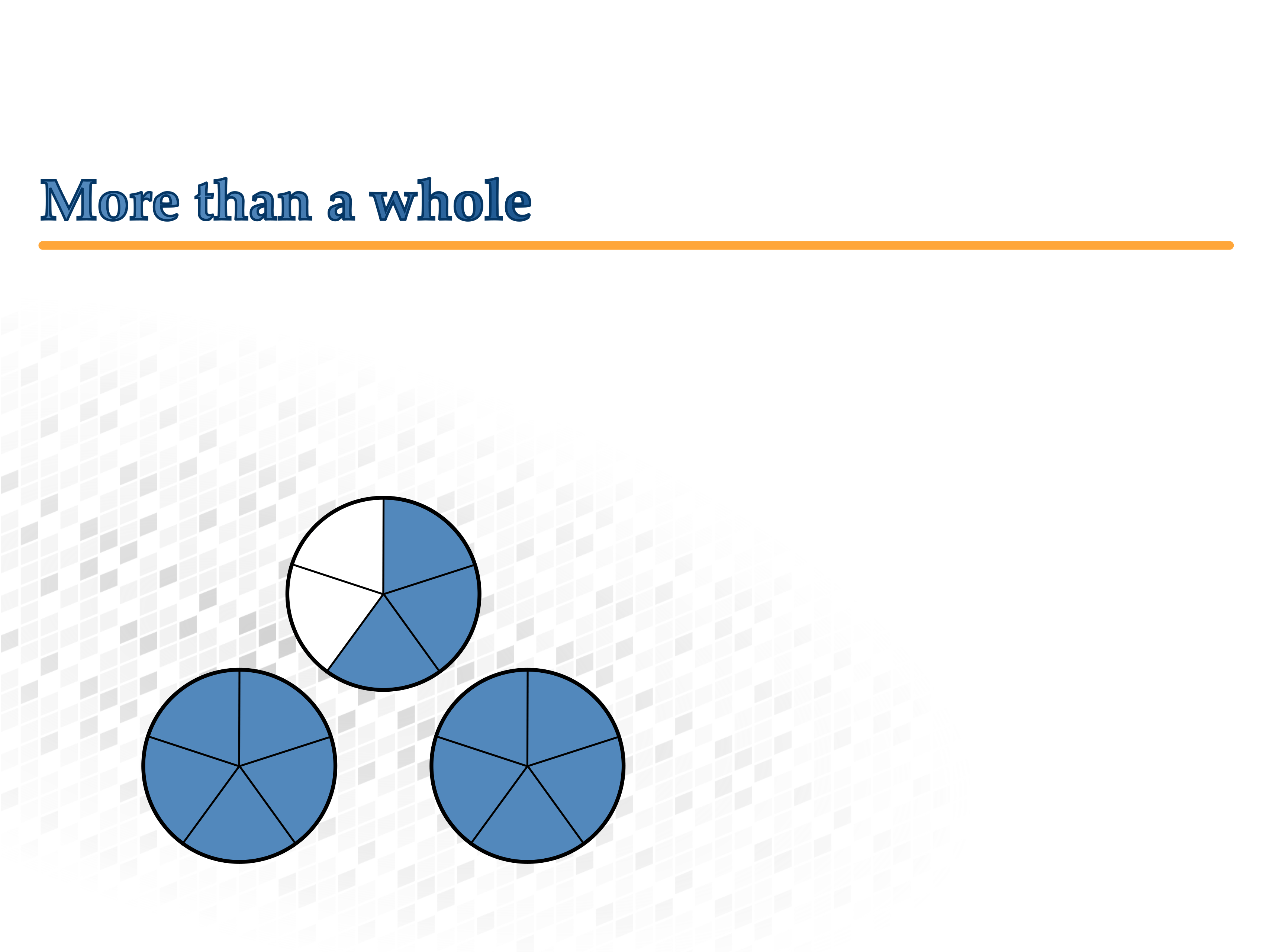
More than a whole

Proper and improper fractions.

The four fractions can be divided into two groups:

  1. Fractions greater than a whole and...
  2. fractions less than a whole.
Decide which group each of the fractions belong to. Then, write down how you would recognize this on the number line. Compare your results with a neighbor.

Strange fractions

The fraction $\frac{11}{3}$ is an improper fraction. On the number line it is to the right of 1.

It is often helpful to know how many whole numbers are in an improper fraction. Mixed numbers Zahlen are a different way of writing improper fractions.

Mixed numbers

A mixed number is a combination of two numbers:

  1. A natural number which tells us how many wholes are in the improper fraction and...
  2. a proper fraction, which tells us the remainder.

Bei $\frac{11}{3}$ would look like this:

Writing an improper fraction as a mixed number is a much shorter way of writing improper fractions:

$$\frac{11}{3}= {\color{#FF8C00}{3\text{ wholes}}} + {\color{#008077}{\frac{2}{3}}}= {\color{#0C5AA6}{3\,\frac{2}{3}}}$$

And without the number line…?

Below you can see another way to convert the improper fraction $\frac{11}{3}$ into the mixed number $3\,\frac23$:

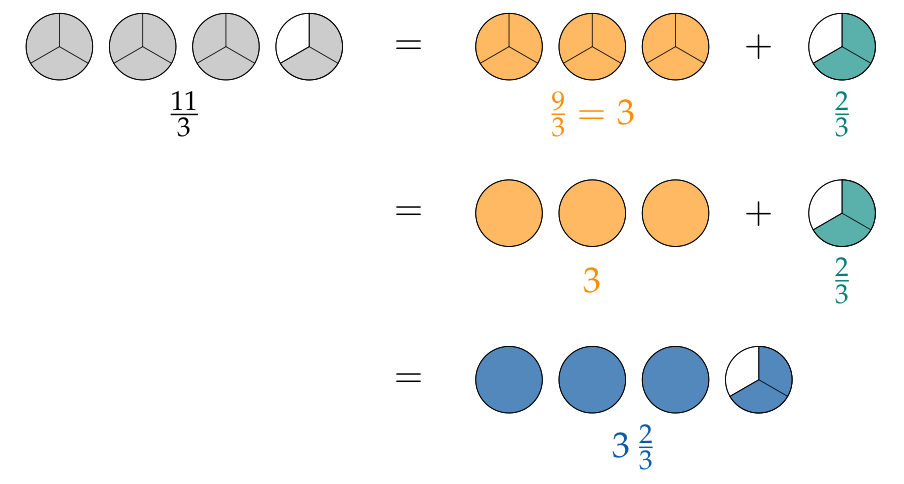
Improper fractions can also be written as mixed numbers:

$$\begin{aligned} \frac{11}{3}&= 11:3= {\color{#FF8C00}3}\text{ R }{\color{#008077}2}\\[1em] \frac{11}{3}&= 11:3= {\color{#FF8C00}3} +{\color{#008077}{\frac23}}= {\color{#0C5AA6}{3\,\frac23}}\end{aligned}$$

With some practice you will be able to do these conversions in your head without writing out all of your calculations.

And the other way around…?

It is also possible to convert a mixed number to an improper fraction:

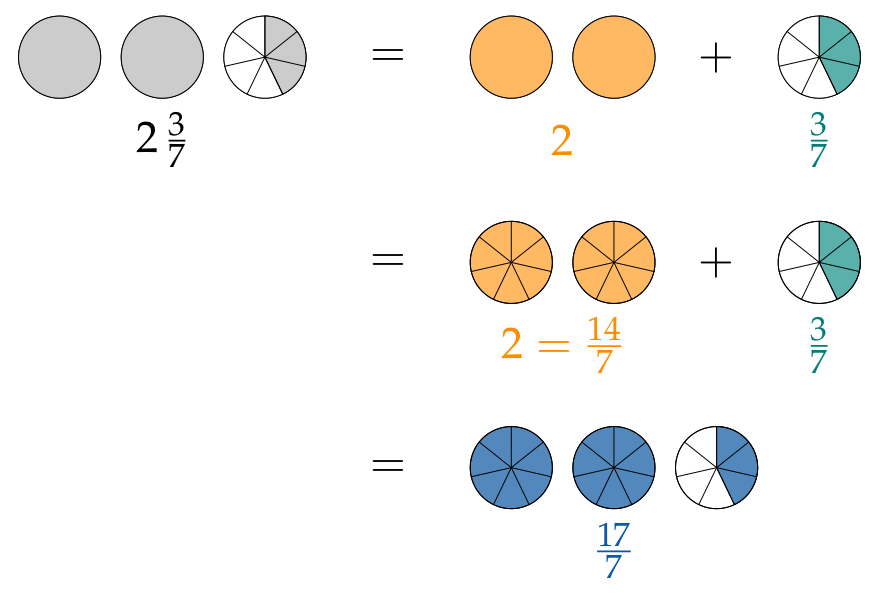
Mixed numbers can also be written as improper fractions:

$$2\,\frac{3}{7}= {\color{#FF8C00}2} +{\color{#008077}{\frac{3}{7}}}= {\color{#FF8C00}{\frac{14}{7}}} +{\color{#008077}{\frac{3}{7}}}= {\color{#0C5AA6}{\frac{17}{7}}}$$

If a fraction’s numerator is greater than the denominator it represents something greater than a whole. This type of fraction is called an improper fraction.

By converting them to mixed numbers we can easily see where they are located on the number line:

$$\frac{10}{3}= 3+\frac13= {\color{#0C5AA6}{3\,\frac13}}$$

The fraction is between 3 and 4 on the number line.

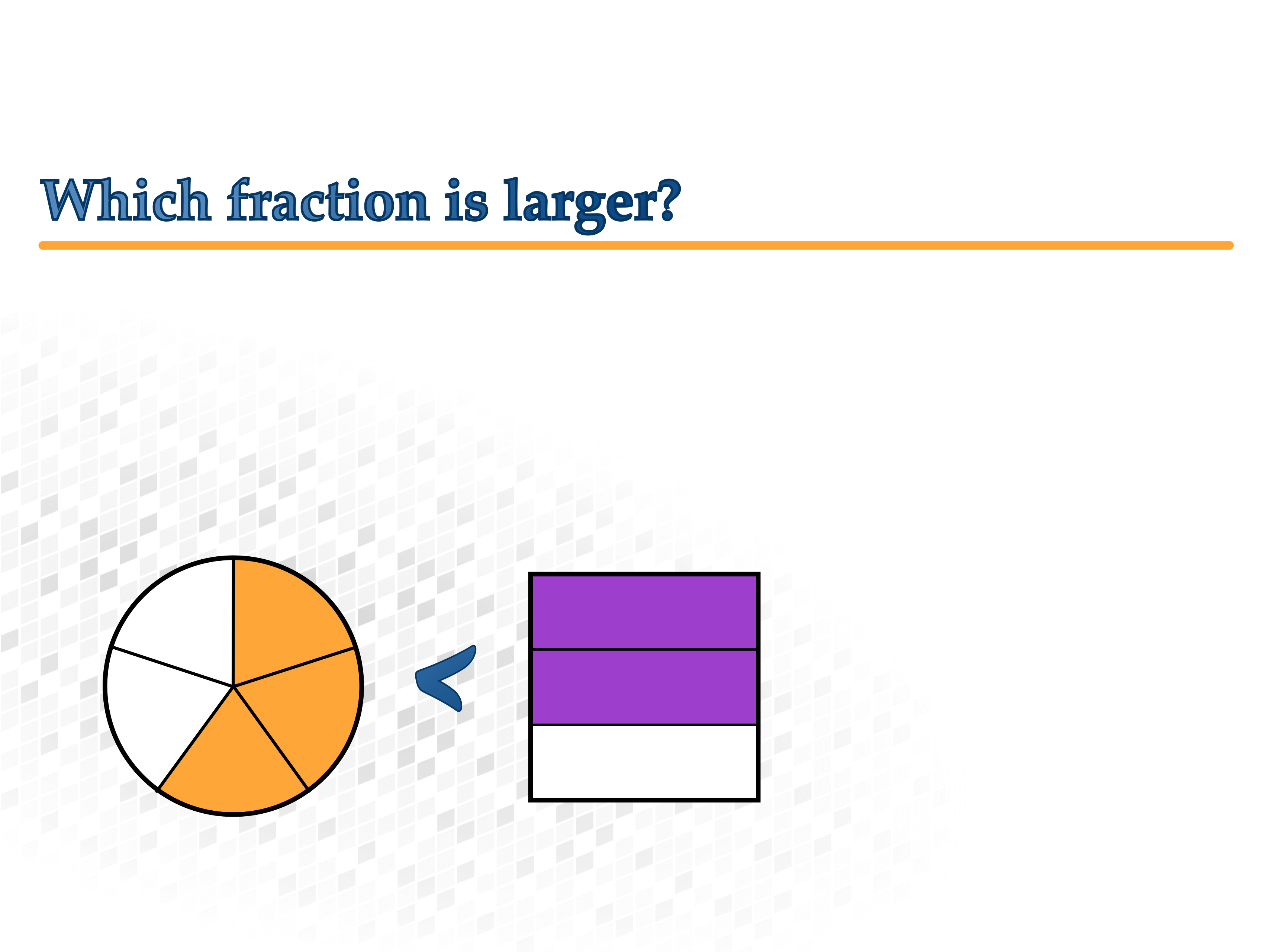
What fraction is larger?

Less or greater than a whole?

It is not hard to determine whether a fraction is less than or greater than a whole. Simply check if it is to the left or right of the 1 on the number line!

Remember

Improper fractions are fractions that are greater than a whole (e. g. $\frac54$ or $\frac97$).

Proper fractions are fractions that are less than a whole (e. g. $\frac34$ or $\frac78$).

Improper fractions (e. g. $\frac65$) are more than a whole.

They are always greater than proper fractions (e. g. $\frac78$):

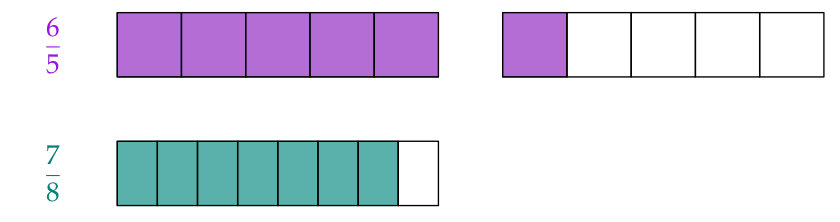$$\text{So, } {\color{#9516E0}{\frac{6}{5}}}>{\color{#008077}{\frac{7}{8}}}.$$

Use this strategy to solve the problem:

Less than or greater than a half?

It is not hard to determine whether a fraction is less than or greater than one half of a whole.

If one fraction is greater than one half (e. g. $\frac47$) and another fraction is less than one half (e. g. $\frac35$), you can easily compare the two:

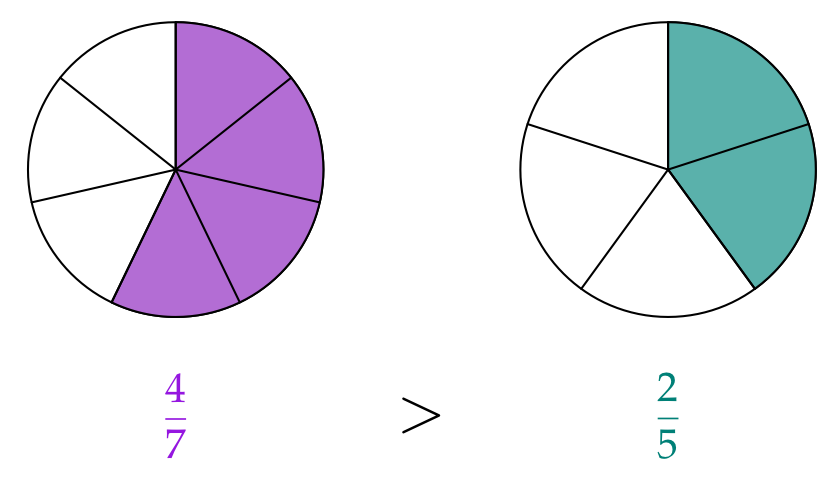
Use this strategy to solve the problem:

Fractions with the numerator 1

To solve the next problems we will need a new strategy:

"The smaller the denominator, the larger the pieces!"

Note

Fractions with the numerator 1 are called unit fractions.

Fractions with the same numerator

You can also use this strategy to compare fractions which have the same numerator.

If the fractions have the same numerator the greater fraction is the one with the smaller denominator.

That is the fraction, where the whole is divided into fewer pieces:

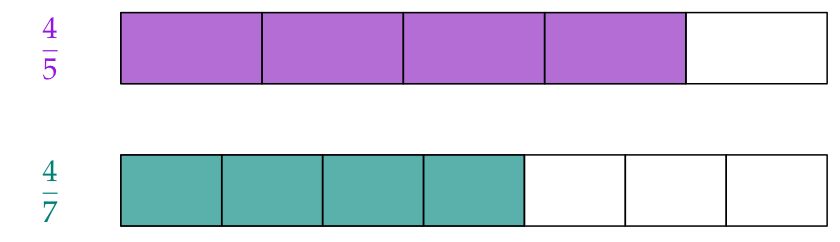$$\text{So, }{\color{#9516E0}{\frac{4}{5}}}>{\color{#008077}{\frac{4}{7}}}.$$

Fractions with the same denominator

On the other hand if the denominators are the same, you simply have to find out which one has more pieces:

"The smaller the numerator, the less pieces there are!"

If two fractions have common denominators you can compare the numerators.

The larger fraction is the one with the greater numerator.

This also just means, that the fraction which has more of the equal-sized pieces is greater:

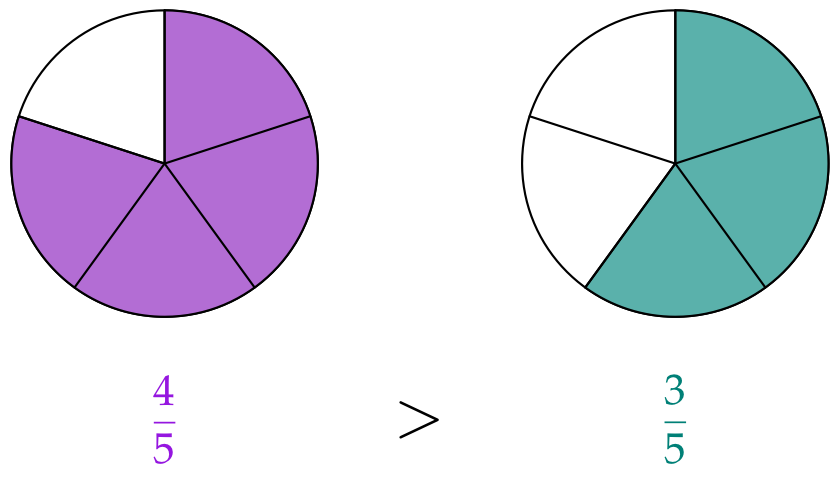
During the next problems pay attention to whether the fractions have common numerators or common denominators.

Time for chocolate

During their lunch break Steve and Francis each buy a bar of chocolate. Afterwards Steve has $\frac14$ and Francis has $\frac{9}{32}$ left.

Finding a common numerator or denominator?

To compare two fractions you can either find a common numerator or a common denominator Often one of the two ways will be easier:

 

Example 1

Which fraction is greater: $\displaystyle\frac{2}{15}$ or $\displaystyle\frac{3}{17}$?

Using a common numerator: $\displaystyle\color{#9516E0}{\frac{6}{45}}<\color{#008077}{\frac{6}{34}}$
Using a common denominator: $\displaystyle\color{#9516E0}{\frac{34}{255}}<\color{#008077}{\frac{45}{255}}$
Beispiel 2

Which fraction is greater: $\displaystyle\frac{13}{16}$ oder $\displaystyle\frac{3}{4}$?

Using a common numerator: $\displaystyle\color{#9516E0}{\frac{39}{48}}>\color{#008077}{\frac{39}{52}}$
Using a common denominator: $\displaystyle\color{#9516E0}{\frac{13}{16}}>\color{#008077}{\frac{12}{16}}$

What is easier?

Find a common numerator or denominator to compare the fractions. Decide for yourself.

Choose whichever strategy you prefer.
Sollte das Widget nicht korrekt dargestellt werden, versuche, es durch einen Klick hier in einem neuen Fenster zu öffnen.

Cookies are used on our website. They allow us to see how many people are using our e-book. They are not used to personally identify website visitors.