Stefan Hoch
Frank Reinhold
Bernhard Werner
Kristina Reiss
Jürgen Richter-Gebert
Fracciones
Preámbulo
Operaciones con fracciones: aprender y comprender
Cuarta reimpresión.
Stefan Hoch,
Frank Reinhold,
Bernhard Werner,
Kristina Reiss,
Jürgen Richter-Gebert
Technical University of Munich, 2018.
Patrocinado por la Fundación Heinz Nixdorf
Traducción: Patricia Haller, Marian Anguela González
Licencia:
Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Citar como:
Hoch, S., Reinhold, F., Werner, B., Reiss, K., Richter-Gebert, J. (2018). Fracciones.Operaciones con fracciones. Aprender y comprender [Web Version]. Múnich, Alemania, Technical University of Munich.
Technical University of Munich
TUM School of Education
Heinz Nixdorf-Chair of Mathematics Education
Arcisstraße 21
80333 Munich
Prólogo
Alice was beginning to get very tired of sitting
by her sister on the bank, and of having nothing
to do: once or twice she had peeped into the
book her sister was reading, but it had no pictures
or conversations in it, »and what is the use
of a book,« thought Alice »without pictures or
conversation?«
Así empieza Lewis Carroll su famoso libro Alice in Wonderland.
Nuestro libro sobre fracciones apenas tiene diálogos pero a cambio muchas imágenes – aún más – imágenes interactivas. Durante la concepción de este iBook hemos prestado consecuentemente atención a enlazar siempre que fuese posible el tema de fracciones, que a veces puede ser bastante complicado y ciertamente no muy intuitivo ... „Son $\frac{13}{15}$ más o menos que $\frac78$?“ – con imágenes, animaciones e interacciones. Nuestro libro sobre fracciones se ha convertido en un libro de trabajo interactivo, en el que hay mucho que hacer. Las tareas pueden resolverse directamente en el iPad y por supuesto también se puede jugar. Áreas de soluciones se pueden rellenar directamente escribiendo a mano con los dedos – siempre y cuando la escritura sea bastante legible.
De este modo se ha convertido este pequeño libro en un experimento en dos formas: un experimento didáctico ciertamente pero además un experimento tecnológico. Creo que podemos decir con buena conciencia que hemos intentado escribir un iBook muy especial. Exactamente un libro interactivo, con ayudas de aprendizaje incorporadas, juegos, tareas, visualizaciones, juegos de memoria, en el que hay que repartir pizza y chocolate.
Deseamos a los lectores, que se diviertan por lo menos tanto como nosotros mientras hemos ideado las tareas.
Munich, marzo 2018
Jürgen Richter-Gebert
Instrucción
Aquí ves un ejemplo de una tarea. Todas las tareas son como esta o parecidas.
¡Pulsa las flechas azules!
Limpiar
Este libro salva tu progreso. Si quieres empezar de nuevo con el practicar, puedes restablecer todas las tareas. Para eso pulsa con el dedo en la flecha a la derecha. Entonces sigue las instrucciones.
Operaciones con fracciones. Aprender y comprender
Repartir una pizza
Anna quiere repartir una pizza con sus cinco amigas. La corta en trozos iguales.
Aquí vuelves a ver la pizza.
Escribir fracciones
Se divide una pizza en ocho trozos iguales. Mia coge tres trozos.
Se dice: „3 octavos“, y se escribe así:
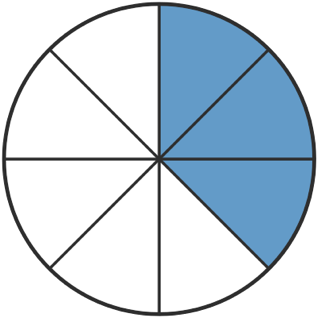
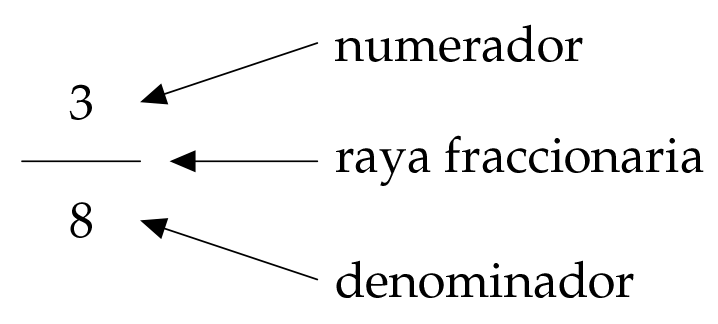
En la representación numérica $\frac38$ aparecen dos números con distinto significado:
„El ocho indica en cuantas partes iguales se divide la pizza. El tres representa cuantas partes del entero se han cogido.“
Las partes de un entero se pueden escribir como una fracción:
El denominador indica en cuantas partes iguales se divide el entero.
El numerador representa cuantas de esas partes se han cogido.
Numerador y denominador están separados por la raya fraccionaria.
Se dice: „3 cuartos“, y se escribe:
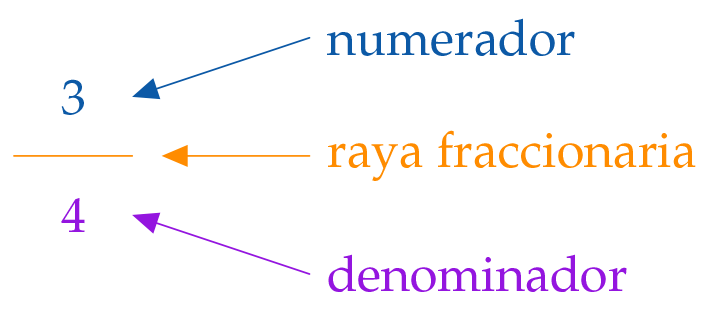
Ten en cuenta
El numerador también puede ser menor, igual o mayor al denominador, por ej.:
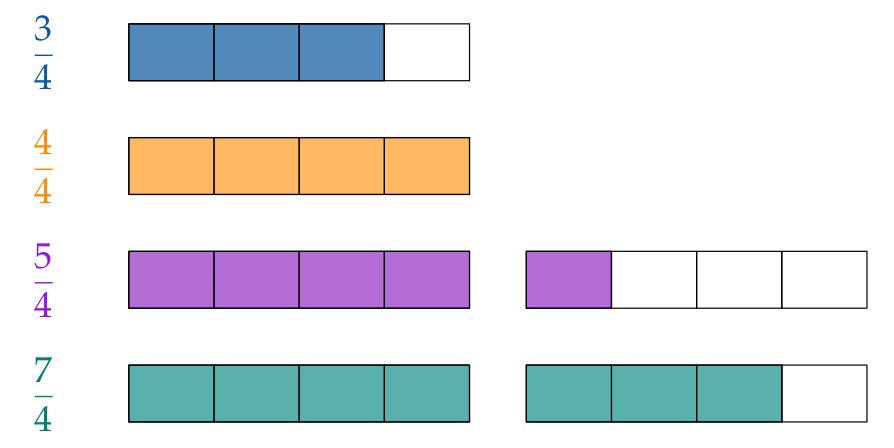
Fracciones así representan más que un entero.
Calcular la parte de algo
Llenar una jarra de agua
En esta jarra cabe un litro de agua. No está llena. Experimenta con la cantidad. Puedes ver que fracción se encuentra en la jarra.
Dividir distancias
Una distancia de $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\textrm{m}$ se obtiene …
- dividiendo una distancia de $1\,\text{m}$ en cuatro partes iguales y después ...
- cogiendo tres de esas partes:
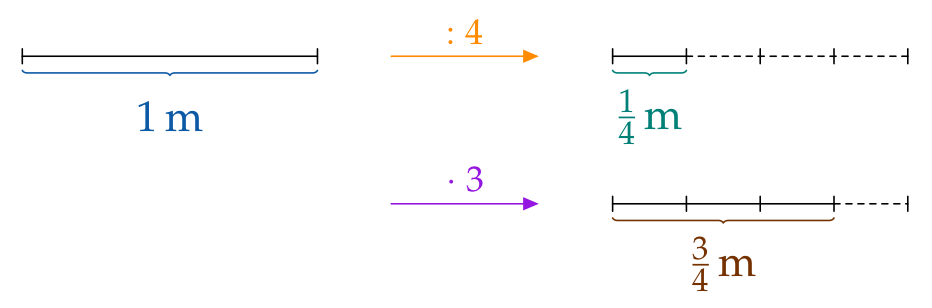
$\frac34\,\text{m}$ son 3 cuartos de un metro (entero).
¿Y sin dibujo ...?
Soluciona la proxima tarea sin hacer un dibujo.
Así se averigua la parte de un entero (la fracción) muy fácilmente:
$$\frac{{\color{#9516E0}5}}{{\color{#FF8C00}7}}\text{ de }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#FF8C00}\,:\,}{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$¿No sabes cómo continuar?
Algunas tareas te ofrecen una pista. Para eso sólo tienes que tocar el „semáforo“ arriba en la esquina derecha de la tarea.
¿Y al revés ...?
Si $\frac13$ de una hora de clase dura 15min, ¿cuánto dura una hora de clase entera?
$$15\,\text{min}\cdot \color{#0C5AA6}{3} = 45\,\text{min}$$Fracciones con el numerador 1 (por ej. $\frac13, \frac12$ o $\frac17$) se llaman fracciones unitarias.
Como acabas de ver se puede calcular el entero original muy fácilmente si la fracción es una fracción unitaria.
Volvemos a usar una distancia para pensar cómo proceder si la fracción no es unitaria.
Regreso a la distancia entera
Si consideramos una longitud de $\frac34\,\text{m}$, se consigue una longitud de un metro ...
- primero dividiendo la distancia en tres partes iguales y después …
- juntando cuatro de esas partes:
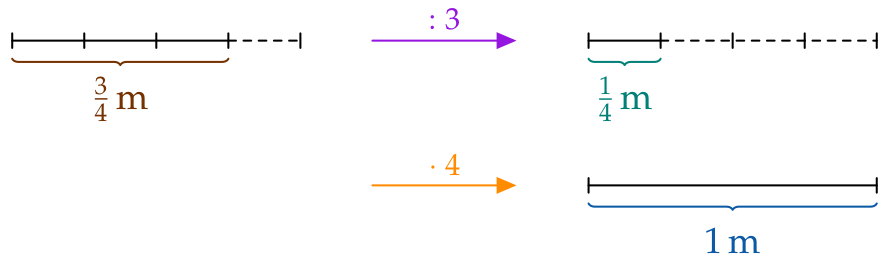
$\frac34\,\text{m}$ son 3 cuartos de un metro (entero).
Si conoces la fracción „$\frac{\color{#9516E0}5}{\color{#FF8C00}7}$“ y la parte de la fracción „$15\,\text{m}$“, puedes averiguar el entero. Básicamente funciona al revés:
$$\Big({{15\,\text{m}}}~{\color{#9516E0}{:5}}\Big){\color{#FF8C00}\cdot}{\color{#FF8C00}7}= 3\,\text{m}{\color{#FF8C00}\cdot}{\color{#FF8C00}7}= {{21\,\text{m}}}$$
Repartir pizza y chocolate
El fabricante de pizza señor Donatello tiene problemas en la cocina.
Además de todo eso cuatro clientes quieren repartir sus pizzas.
Resumen
Ya que los cuatro clientes quieren repartir las pizzas justamente entre ellos, cada uno recibe lo mismo.
Al final cada cliente tiene $\frac14$ de tres pizzas. Eso equivale a $\frac34$ de una pizza.
Se reparten tres barras de chocolate entre 4 niños
A Tim, Karl, Willi y Gabi les encantan las barras de chocolate.
Dividir distancias de diferentes formas
La fracción $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\text{m}$ también se puede obtener así:
- Divide una distancia de $3\,\text{m}$ en 4 partes iguales y …
- toma una parte.
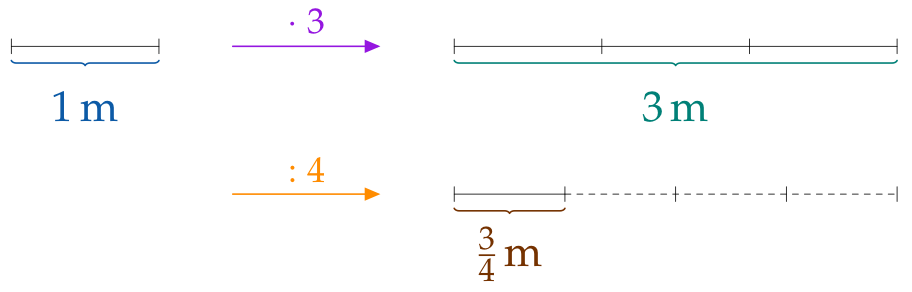
$\frac34\,\text{m}$ también son $\frac14$ de tres metros (enteros).
¿Y sin dibujo ...?
Soluciona la próxima tarea sin hacer un dibujo.
La fracción $\frac{\color{#9516E0}5}{\color{#FF8C00}7}$ de $21\,\text{m}$ se puede calcular de dos maneras distintas:
$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ de }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#9516E0}\cdot}{\color{#9516E0}5}\Big)~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= 105\,{\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= {15\,{\text{m}}}$$o
$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ de }{{21\,\text{m}}}= \Big({21\,\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$Los dos cálculos son correctos. Se obtiene el mismo resultado.
Los deberes de matemáticas de Paul
Paul está en cuarto curso, su hermano Max ya en sexto. Paul hace sus deberes y se los dá a Max para que los corrija:
Dividir cualquier número
Hasta ahora no has podido solucionar tareas de división con un divisor mayor que el dividendo. Para eso usaste la notación con resto:
$$\begin{aligned}3:11 &= 0\ \text{R}\ 3\\ 5:6& = 0\ \text{R}\ 5\end{aligned}$$Con las fracciones no hace falta usar la notación con resto. La division ${\color{#0C5AA6}3}:\color{#FF8C00}{11}$ significa:
„Divide 3 enteros en 11 trozos iguales.“
El resultado es la fracción $\frac{\color{#0C5AA6}{3}}{\color{#FF8C00}{11}}$. O sea: $$\begin{aligned}3:11 &= \frac{3}{11}\\[1em] 5:6& = \frac56\end{aligned}$$
Puedes dividir todos los números naturales por otros, no importa si hay resto. Escribes la solución como fracción.
La fracción $\frac{{\color{#0C5AA6}3}}{{\color{#FF8C00}4}}$ es otra manera para escribir el cociente ${\color{#0C5AA6}3}:{\color{#FF8C00}4}$.
Con fracciones se pueden dividir todos los números naturales entre ellos, por ej.:
$3:4=\frac34,\quad 5:2=\frac52,\quad 3:7=\frac37,\quad 5:6=\frac56$
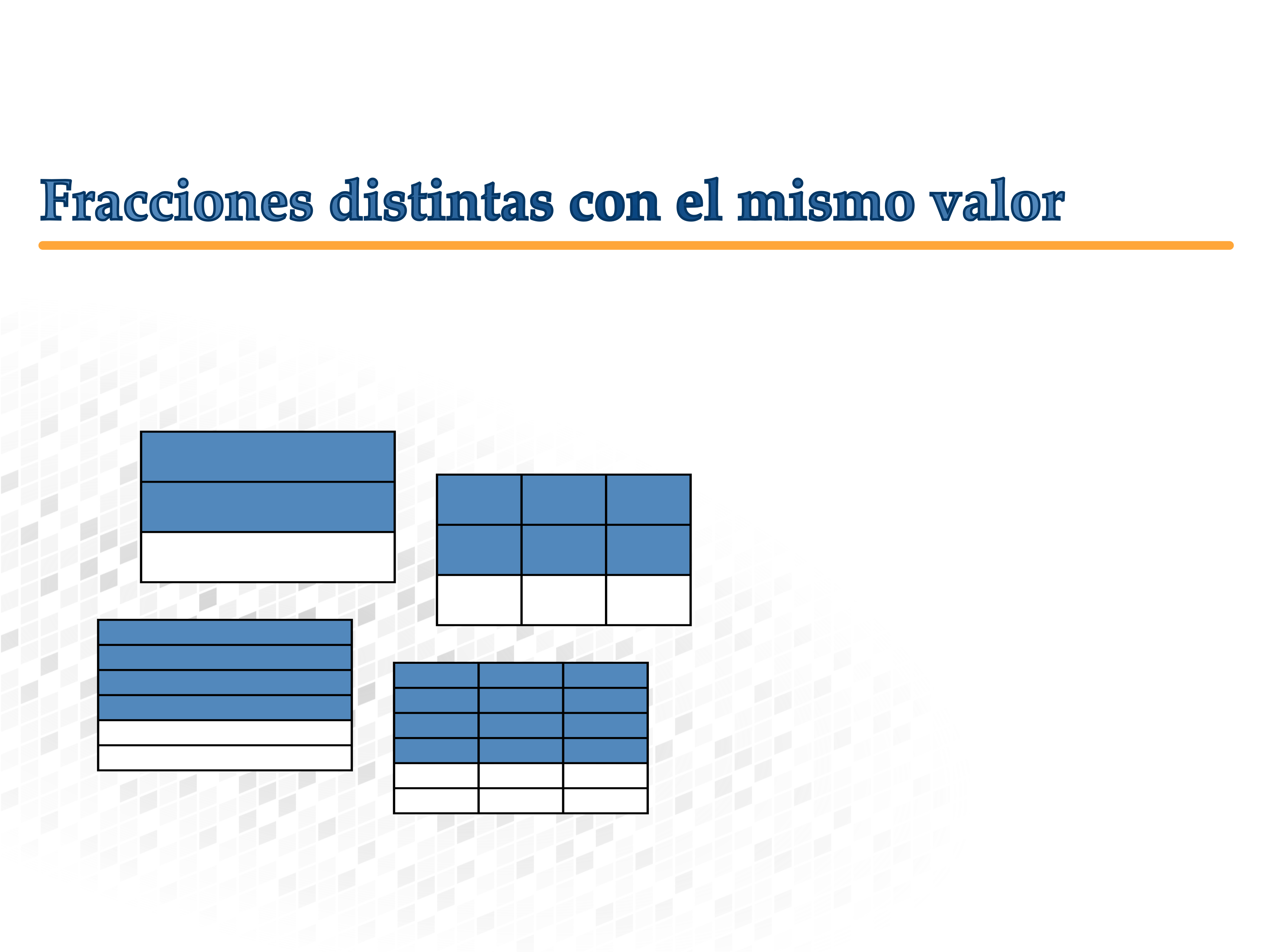
Fracciones distintas con el mismo valor
Se dobla un papel
Recorta un cuadrado de una hoja de papel. Pinta la mitad del cuadrado.
Fracciones distintas que tienen el mismo valor
Encuentra con ayuda del widget distintas fracciones que se refieren a la misma parte del círculo.
Y ahora sin dibujo …
Maria dice: „Me he dado cuenta de que siempre tengo que hacer lo mismo arriba y abajo.“
¿A qué se refiere Maria?
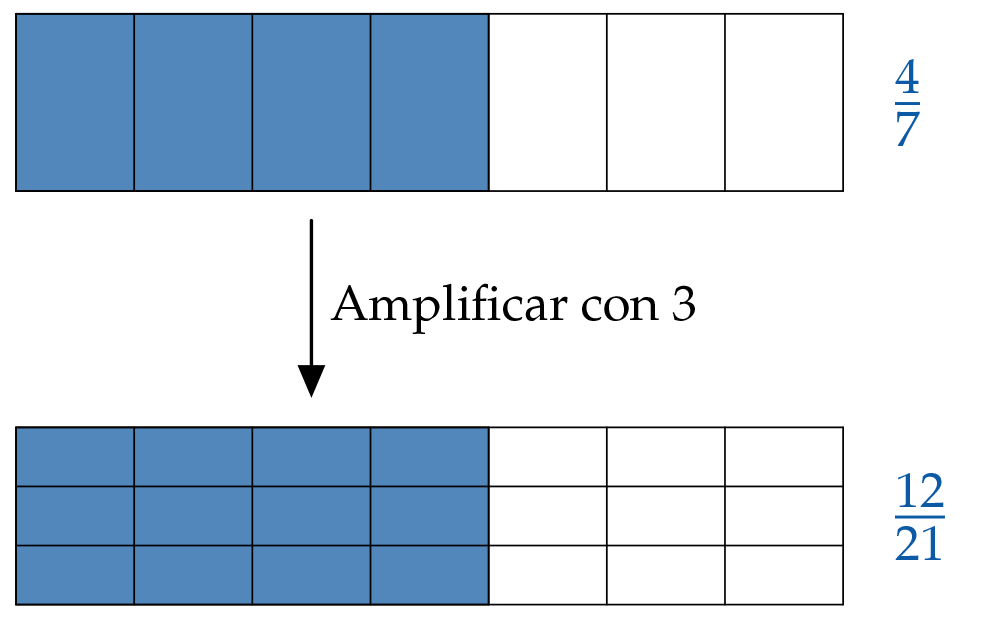
Amplificar significa: multiplicar el numerador y el denominador con el mismo número.
Escribimos el número con el que hemos ampificado la fracción sobre el signo de igualdad:
$$\frac47 \begin{matrix} \color{#0C5AA6}3\\ =\\ \phantom{3} \end{matrix} \frac{4{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}{7{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}=\frac{12}{21} $$Amplificando la división, esta se vuelve más fina:
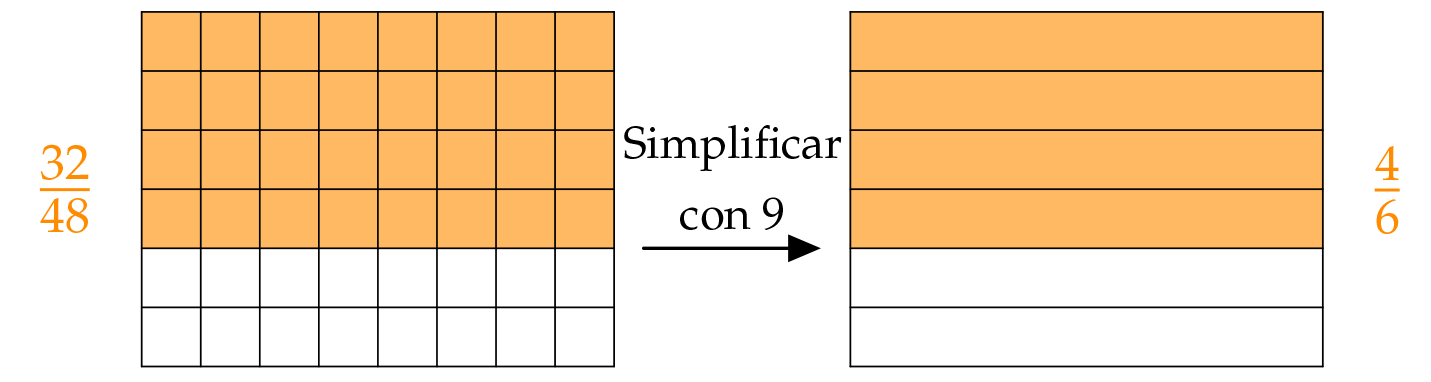
Simplificar significa: dividir el numerador y el denominador por el mismo número.
Escribimos el número con el que hemos simplificado la fracción debajo del signo de igualdad:
$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#FF8C00}8 \end{matrix} \frac{32{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}{48{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}= \frac{4}{6} $$Simplificando la division se vuelve menos fina:
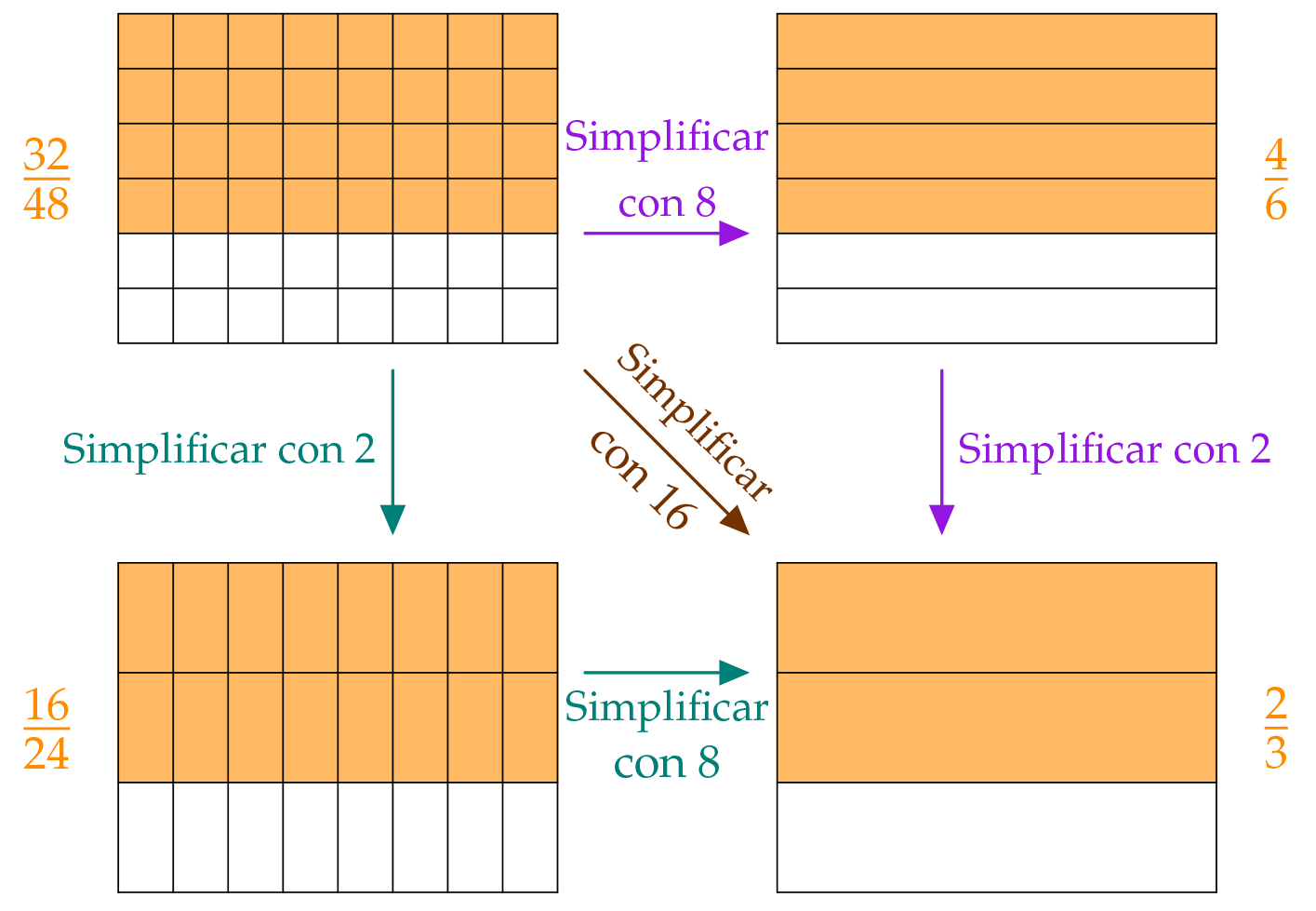
Continuar simplificando
Puedes simplificar fracciones con un divisor común del numerador y denominador.
Los divisores comunes del numerador „32“ y el denominador „48“ de la fracción $\frac{32}{48}$ son 8, 2 und 16. Por eso podemos simplificar la fracción $\frac{32}{48}$ de maneras distintas:
Y ahora sin dibujo …
También lo podemos apuntar en forma de calculación:
$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#9516E0}8 \end{matrix} \frac{32{\,\color{#9516E0}:\,}{\color{#9516E0}8}}{48{\,\color{#9516E0}:\,}{\color{#9516E0}8}}= \frac{4}{6} \begin{matrix} \phantom{2}\\ =\\ \color{#9516E0}2 \end{matrix} \frac{4{\,\color{#9516E0}:\,}{\color{#9516E0}2}}{6{\,\color{#9516E0}:\,}{\color{#9516E0}2}}= \frac23 $$o
$$ \frac{32}{48} \begin{matrix} \phantom{2}\\ =\\ \color{#008077}2 \end{matrix} \frac{32{\,\color{#008077}:\,}{\color{#008077}2}}{48{\,\color{#008077}:\,}{\color{#008077}2}}= \frac{16}{24} \begin{matrix} \phantom{8}\\ =\\ \color{#008077}8 \end{matrix} \frac{16{\,\color{#008077}:\,}{\color{#008077}8}}{24{\,\color{#008077}:\,}{\color{#008077}8}}= \frac23 $$o
$$ \frac{32}{48} \begin{matrix} \phantom{16}\\ =\\ \color{#753200}{16} \end{matrix} \frac{32{\,\color{#753200}:\,}{\color{#753200}{16}}}{48{\,\color{#753200}:\,}{\color{#753200}{16}}}= \frac23 $$El numerador y el denominador de la fracción $\frac23$ no tienen un divisor común. Una fracción así se llama irreducible.
Amplificar y simplificar no cambia el valor decimal de una fracción.
Una fracción sólo puede ser simplificada por un divisor común del numerador y denominador.
Si el numerador y el denominador no tienen un divisor común, la fracción se llama irreducible.
Fracciones en la recta numérica
Desenrollar un círculo
¿Qué significan fracciones en la recta numérica?
Reducir un rectángulo
Tambien puedes imaginarte la recta numérica como un „rectángulo reducido“.
Fracciones se pueden representar en una recta numérica. Además puedes imaginarte la recta numérica como un círculo desenrollado:
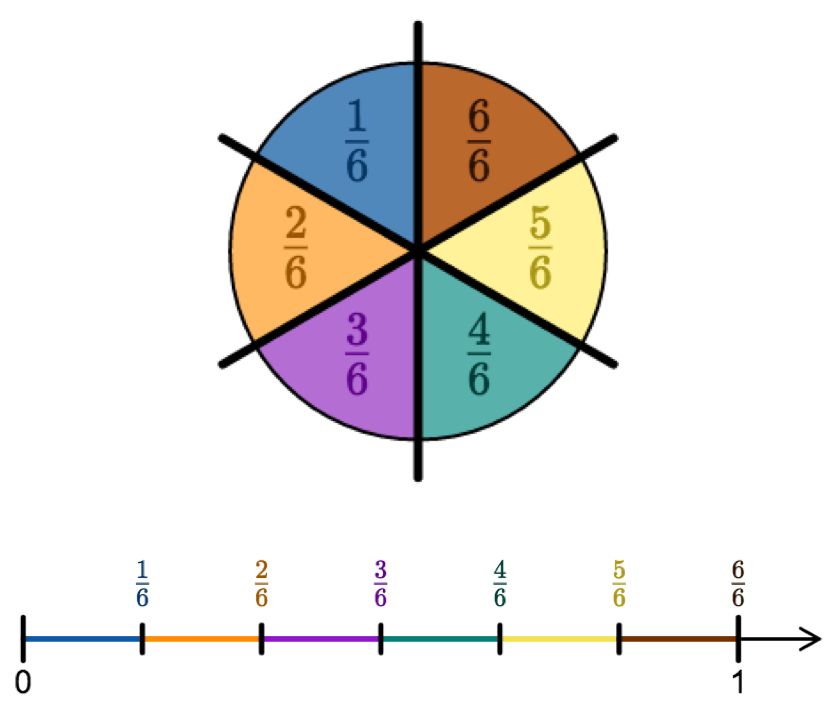
Fracciones con un valor menor que un entero se llaman fracciones propias. En la recta numérica se encuentran entre el 0 y el 1. Su numerador es menor que su denominador.
¿Y a la derecha del 1?
A la derecha del 1 todavia hay espacio sin fin. Aquí se encuentran fracciones que son mayores que un entero.
Fracciones también pueden representar más que un entero. En la recta numérica se representa así:
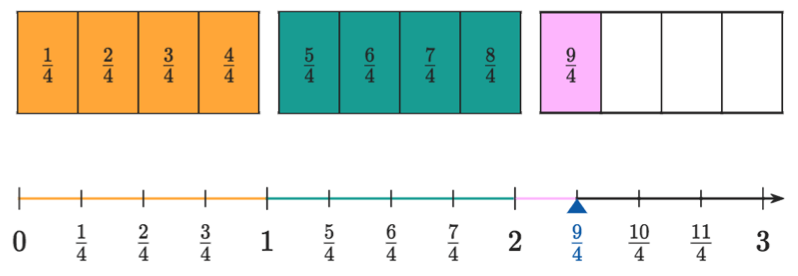
Fracciones que representan más que un entero se llaman fracciones impropias. En la recta numérica se encuentran a la derecha del 1. Su numerador es mayor que el denominador.
¿Y a la derecha del 1?
A la derecha del 1 todavia hay espacio sin fin. Aquí se encuentran fracciones que son mayores que un entero.
Cuando la distribución en la recta numérica no es suficiente hay que refinarla:
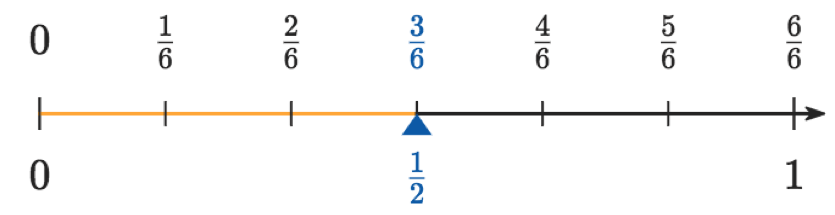
¡¿Sitio ocupado?!
Algunas fracciones comparten sitio en la recta numérica:
En la tarea has visto que las fracciones $\frac13$ y $\frac26$ se encuentran en el mismo sitio en la recta numérica. Lo mismo occurió con las fracciones $\frac{10}{6}$ y $\frac53$.
Si piensas en el capitulo anterior te daras cuenta por qué comparten el mismo sitio esas fracciones:
$$ \frac13 \begin{matrix} 2\\ =\\ \phantom{2} \end{matrix} \frac26 \quad \text{ und } \quad \frac{10}6 \begin{matrix} \phantom{2}\\ =\\ 2 \end{matrix} \frac{5}{3} $$Las fracciones son equivalentes, por qué se pueden convertir una en la otra amplificando o simplificando.
A cada fracción le pertenece un punto en la recta numérica. ¡Fracciones equivalentes comparten el mismo sitio!
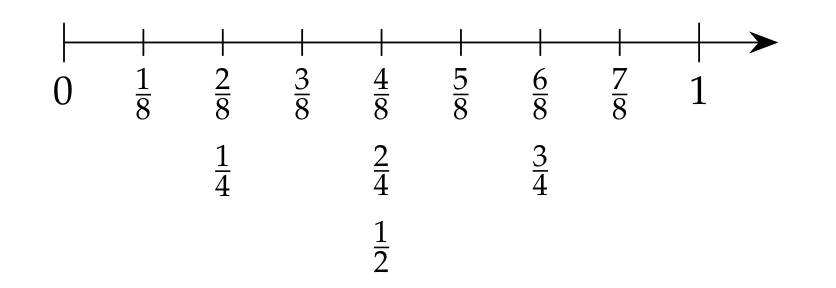
Más que un entero
Puedes dividir las cuatro fracciones en dos grupos:
- Partes que son más grandes que un entero y ...
- partes que son más pequeñas que un entero.
Fracciones raras
La fracción $\frac{11}{3}$ es una fracción impropia. En la recta numérica se encuentra a la derecha del 1.
Muchas veces es útil saber cuantos enteros incluye una fracción impropia. Para eso existe una forma especial de escribir: los números mixtos.
Números mixtos
Un número mixto consta de dos partes:
- Un número natural, que indica cuantos enteros incluye la fracción impropia y ...
- una fracción propia, que indica el resto.
Con $\frac{11}{3}$ se representa así:
En forma de números mixtos podemos escribir fracciones impropias de una forma más corta:
$$\frac{11}{3}= {\color{#FF8C00}{3\text{ enteros}}} + {\color{#008077}{\frac{2}{3}}}= {\color{#0C5AA6}{3\,\frac{2}{3}}}$$¿Y sin recta numérica?
Aquí ves otra opción para convertir la fracción impropia $\frac{11}{3}$ en el número mixto $3\,\frac23$:
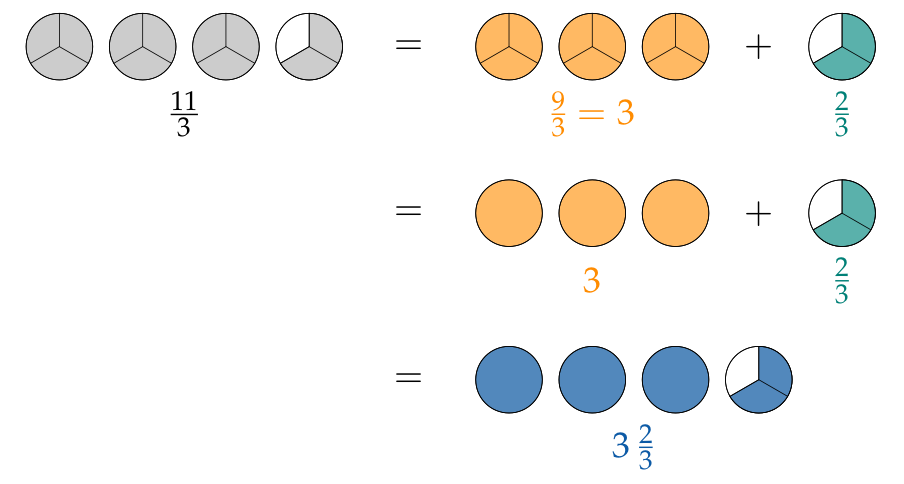
Fracciones impropias también se pueden escribir como números mixtos:
$$\begin{aligned} \frac{11}{3}&= 11:3= {\color{#FF8C00}3}\text{ R }{\color{#008077}2}\\[1em] \frac{11}{3}&= 11:3= {\color{#FF8C00}3} +{\color{#008077}{\frac23}}= {\color{#0C5AA6}{3\,\frac23}}\end{aligned}$$Con un poco de práctica puedes hacer la transformación mentalmente. No tienes que escribir los pasos matemáticos.
¿Y al revés?
También podemos volver a convertir un número mixto en una fracción impropia:
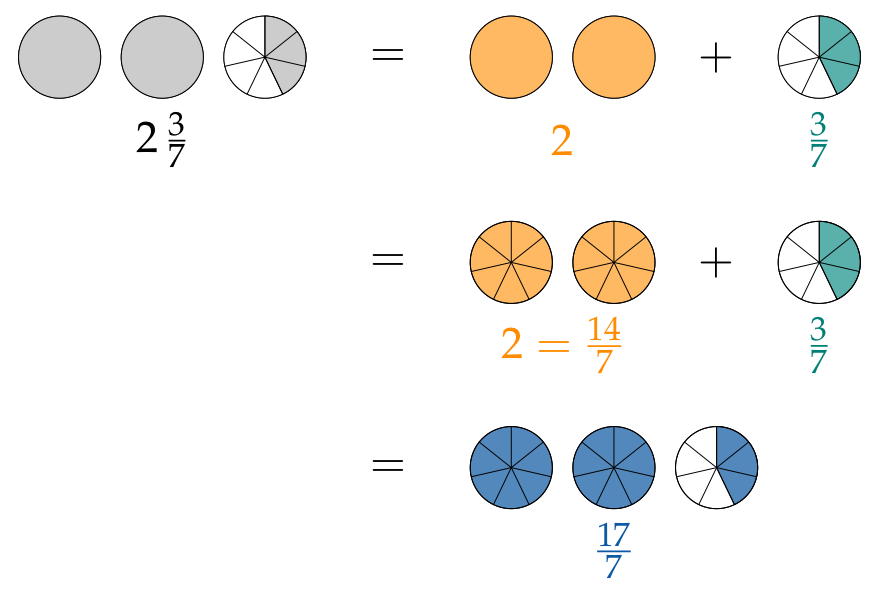
Se pueden volver a escribir números mixtos como fracciones impropias:
$$2\,\frac{3}{7}= {\color{#FF8C00}2} +{\color{#008077}{\frac{3}{7}}}= {\color{#FF8C00}{\frac{14}{7}}} +{\color{#008077}{\frac{3}{7}}}= {\color{#0C5AA6}{\frac{17}{7}}}$$Fracciones con un numerador mayor al denominador representan más que un entero. Se llaman fracciones impropias.
Si las escribimos como números mixtos sabemos inmediatamente donde se encuentran en la recta numérica:
$$\frac{10}{3}= 3+\frac13= {\color{#0C5AA6}{3\,\frac13}}$$Se encuentra entre 3 y 4 en la recta numérica.
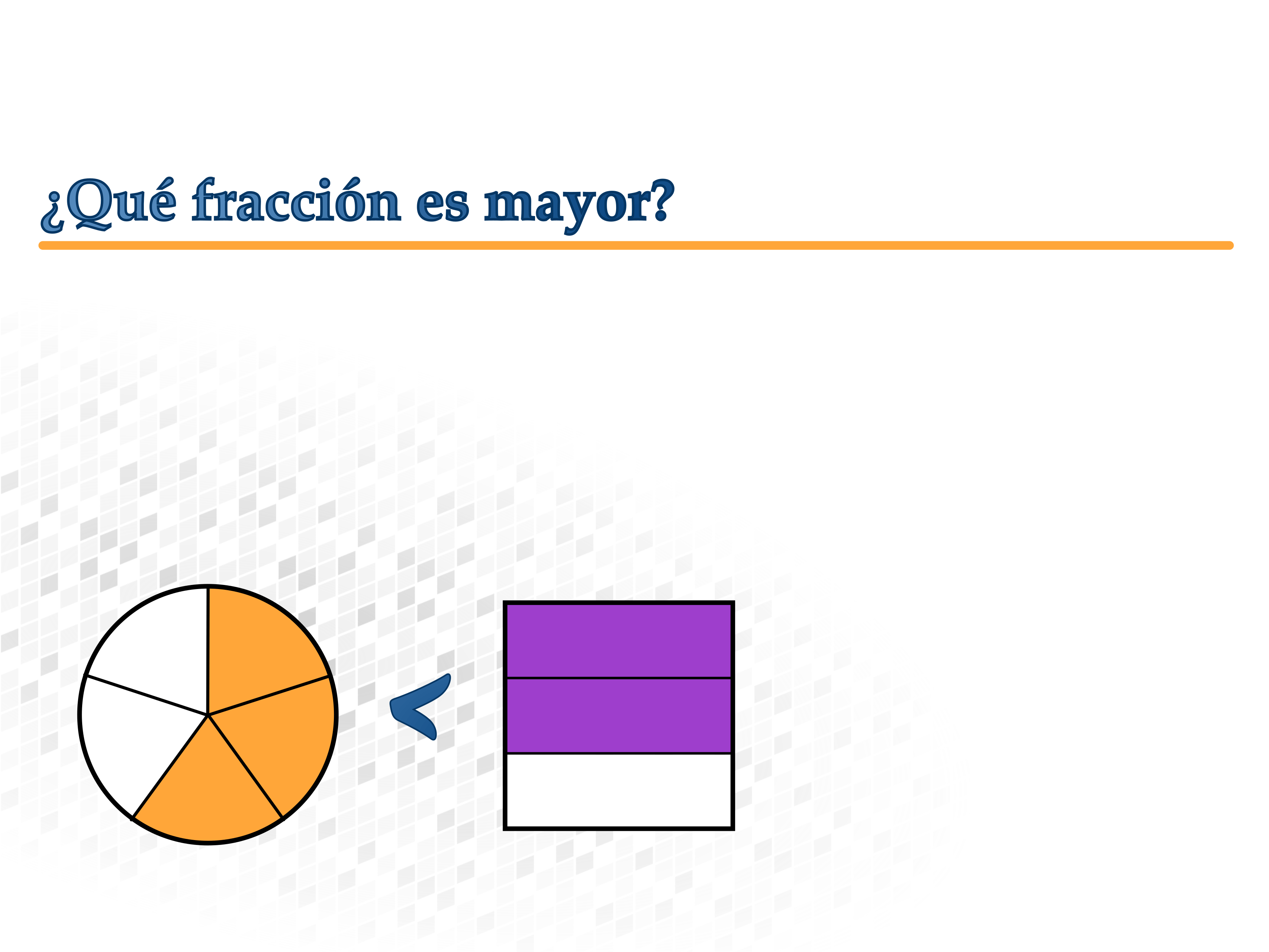
¿Qué fracción es mayor?
¿Menos o más qué un entero?
Si una fracción es menor o mayor que un entero se puede decidir fácilmente: ¿Se encuentra a la izquierda o a la derecha del 1?
Un recordatorio
Fracciones impropias son fracciones que son mayores que un entero (por ej. $\frac54$ o $\frac97$).
Fracciones propias son fracciones que son menores que un entero (por ej. $\frac34$ o $\frac78$).
Fracciones impropias (por ej. $\frac65$) son mayores que un entero.
Siempre son mayores que fracciones propias (por ej. $\frac78$)
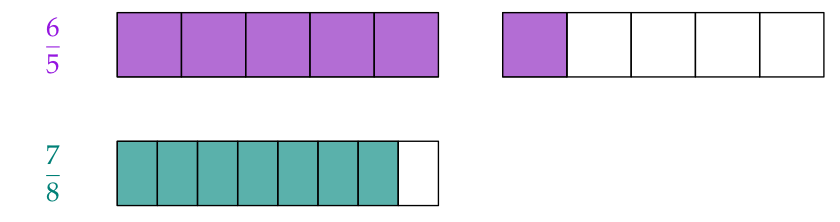$$\text{Entonces }{\color{#9516E0}{\frac{6}{5}}}>{\color{#008077}{\frac{7}{8}}}.$$
Ultiliza esta estrategia para solucionar la tarea:
¿Más o menos que la mitad?
Si una fracción representa más o menos que la mitad de un entero puede averiguarse fácilmente.Cuando una fracción es mayor que la mitad (por ej. $\frac47$) y otra menor que la mitad (por ej. $\frac35$) se pueden comparar fácilmente:
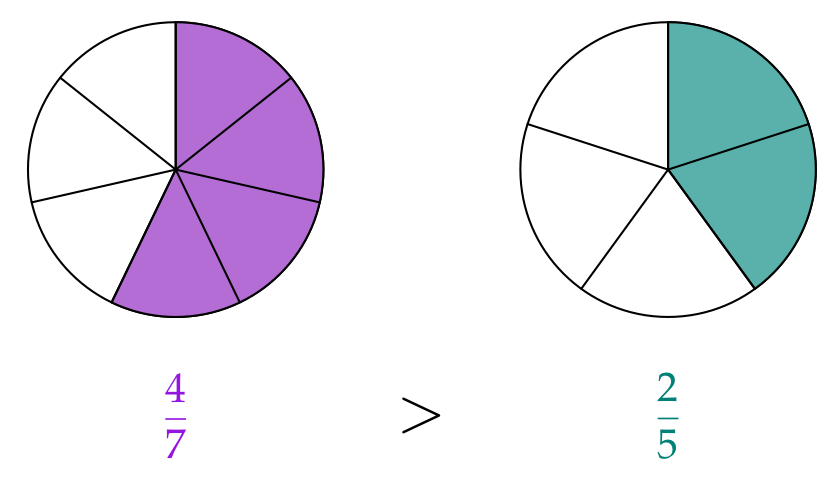
Ultiliza esta estrategia para solucionar las tareas:
Fracciones con el numerador 1
Para las proximas tareas necesitas una nueva estrategia:
„¡Cuánto más pequeño el denominador, más grande los trozos!“
Por cierto
Fracciones con el numerador 1 se llaman fracciones unitarias.
Fracciones con el mismo numerador
La nueva estrategia también funciona para fracciones con el mismo numerador:
Entre fracciones con el mismo numerador la mayor es la que tiene el denominador menor.
O sea la fracción que está partida en menos partes:
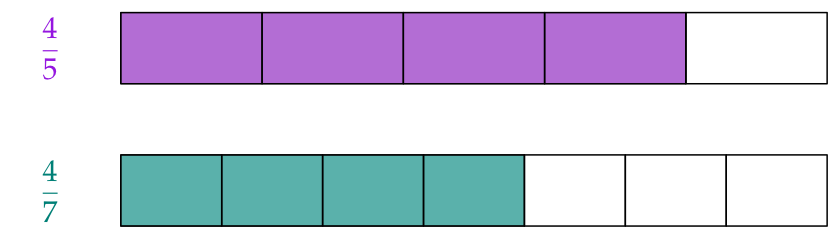$$\text{Entonces }{\color{#9516E0}{\frac{4}{5}}}>{\color{#008077}{\frac{4}{7}}}.$$
Fracciones con el mismo denominador
Si el denominador es igual solamente tienes que averiguar que fracción representa más partes:
„¡Cuanto más pequeño el numerador, menos partes!“
Fracciones con el mismo denominador se llaman fracciones homogéneas.
Entre fracciones homogéneas la fracción mayor es la que tiene el numerador más grande.
O sea la fracción que tiene más cantidad de las partes iguales:
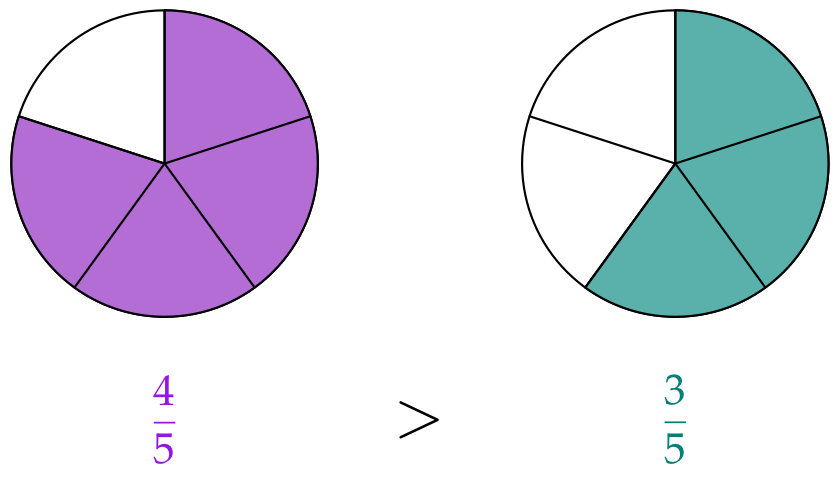
En la proxima tarea tienes que fijarte si las fracciones tienen el mismo numerador o el mismo denominador.
Comer chocolate
En el recreo Steffen y Franziska se compran cada uno una tableta de chocolate. A Steffen le sobra $\frac{9}{32}$ del chocolate y a Franziska $\frac14$.
¿Obtener el mismo numerador o denominador?
Para comparar dos fracciones puedes buscar un numerador común o un denominador común. Muchas veces una variante es la más fácil:
Ejemplo 1
¿Qué fracción es mayor, $\displaystyle\frac{2}{15}$ o $\displaystyle\frac{3}{17}$?
| Con el mismo numerador: | $\displaystyle\color{#9516E0}{\frac{6}{45}}<\color{#008077}{\frac{6}{34}}$ |  |
| Con el mismo denominador: | $\displaystyle\color{#9516E0}{\frac{34}{255}}<\color{#008077}{\frac{45}{255}}$ |  |
Ejemplo 2
¿Qué fracción es mayor, $\displaystyle\frac{13}{16}$ o $\displaystyle\frac{3}{4}$?
| Con el mismo numerador: | $\displaystyle\color{#9516E0}{\frac{39}{48}}>\color{#008077}{\frac{39}{52}}$ | |
| Con el mismo denominador: | $\displaystyle\color{#9516E0}{\frac{13}{16}}>\color{#008077}{\frac{12}{16}}$ | |
¿Qué es más fácil?
Para comparar las fracciones, estas tienen que tener el mismo numerador o denominador. Decide tu mismo.