Stefan Hoch
Frank Reinhold
Bernhard Werner
Kristina Reiss
Jürgen Richter-Gebert
Bruchrechnen
Einleitung
Bruchrechnen. Bruchzahlen & Bruchteile greifen & begreifen
4. überarbeitete Auflage
Stefan Hoch,
Frank Reinhold,
Bernhard Werner,
Kristina Reiss,
Jürgen Richter-Gebert
Technische Universität München, 2018.
Gefördert von der Heinz-Nixdorf-Stiftung
Lizenzierung:
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung – Nicht kommerziell – Keine Bearbeitungen 4.0 International Lizenz.
Vorgeschlagene Zitation:
Hoch, S., Reinhold, F., Werner, B., Reiss, K., Richter-Gebert, J. (2018). Bruchrechnen. Bruchzahlen & Bruchteile greifen & begreifen [Web Version] (4. Aufl.). München, Technische Universität München.
Technische Universität München
TUM School of Education
Heinz Nixdorf-Stiftungslehrstuhl für Didaktik der Mathematik
Arcisstraße 21
80333 München
Vorwort
Alice was beginning to get very tired of sitting
by her sister on the bank, and of having nothing
to do: once or twice she had peeped into the
book her sister was reading, but it had no pictures
or conversations in it, »and what is the use
of a book,« thought Alice »without pictures or
conversation?«
So beginnt Lewis Carroll sein berühmtes Buch Alice in Wonderland.
Unser Buch zu Bruchzahlen hat zwar kaum Dialoge, aber dafür um so mehr Bilder – mehr noch – interaktive Bilder. Wir haben bei der Konzeption dieses iBooks konsequent darauf geachtet, wo immer es möglich war, das manchmal etwas sperrige Thema der Bruchzahlen – das zugegebenermaßen auch unintuitiv sein kann ... „Ist $\frac{13}{15}$ jetzt größer oder kleiner als $\frac78$?“ – mit Bildern, Animationen und Interaktionen zu verknüpfen. Unser Buch zu Bruchzahlen ist ein interaktives Arbeitsbuch geworden, in dem es viel zu tun gibt. Aufgaben – und natürlich auch Spiele – können direkt auf dem iPad bearbeitet und gespielt werden. Lösungsfelder können direkt mit dem Finger in eigener Handschrift ausgefüllt werden – immer vorausgesetzt, sie ist einigermaßen lesbar.
Auf diese Weise ist dieser kleine Band in zweifacher Weise zum Experiment geworden. Ein fachdidaktisches Experiment, das ist klar, aber auch ein technologisches Experiment. Ich glaube, wir können guten Gewissens sagen, dass wir versucht haben ein iBook der ganz besonderen Art zu schreiben. Eben ein interaktives, mit eingebauten Lernhilfen, Spielen, Aufgaben, Visualisierungen, Memories, in dem Pizza und Schokolade verteilt werden müssen.
Wir wünschen den Leserinnen und Lesern mindestens ebenso viel Spaß, wie wir beim Austüfteln der Aufgaben hatten.
München im März 2018
Jürgen Richter-Gebert
Anleitung
Hier siehst du ein Beispiel einer Aufgabe. Alle sehen so oder so ähnlich aus.
Tippe auf die blauen Pfeile!
Aufgaben zurücksetzen
In diesem Buch wird dein Fortschritt gespeichert. Wenn du mit dem Üben ganz von vorne beginnen willst, kannst du alle Aufgaben auch zurück setzen. Tippe dazu mit dem Finger auf den Pfeil rechts. Folge dann den Anweisungen.
Bruchzahlen & Bruchteile greifen & begreifen
Eine Pizza wird geteilt
Anna möchte eine Pizza mit ihren fünf Freundinnen teilen. Sie schneidet sie in gleich große Stücke.
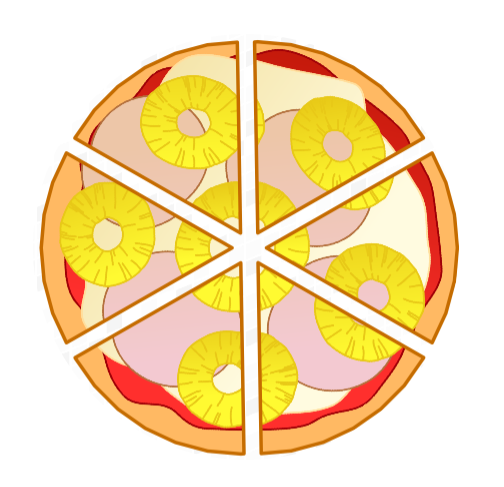
Hier siehst du die Pizza noch einmal.
Brüche schreiben
Eine Pizza wird in acht gleich große Stücke geteilt. Mia nimmt davon drei Stücke.
Man sagt: „3 Achtel“, und schreibt kurz:
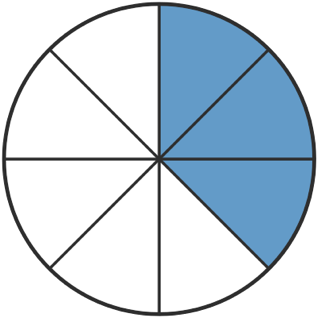
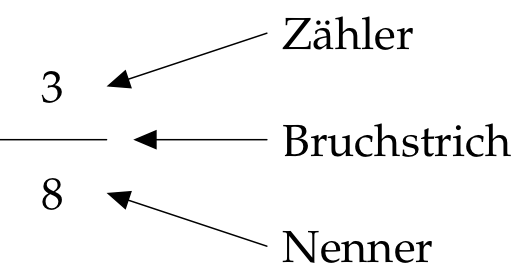
In der neuen Schreibweise $\frac38$ kommen zwei Zahlen mit unterschiedlicher Bedeutung vor:
„Die Acht sagt, in wie viele gleich große Teile man die Pizza teilt. Die Drei gibt an, wie viele dieser Teile man davon nimmt.“
Teile von Ganzen können in der Bruchschreibweise geschrieben werden:
Der Nenner gibt an, in wie viele gleich große Teile das Ganze zerlegt wird.
Der Zähler sagt, wie viele dieser Teile genommen werden.
Zähler und Nenner werden durch den Bruchstrich getrennt.
Man sagt: „3 Viertel“, und schreibt:
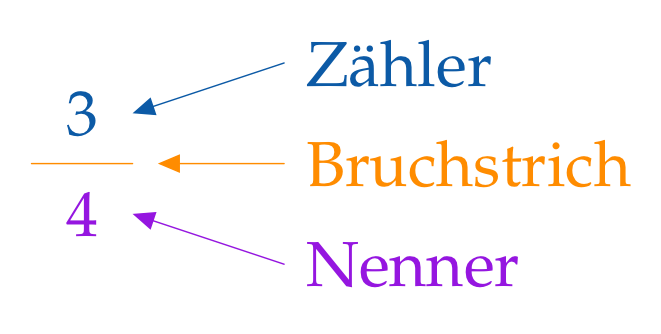
Und noch ein Hinweis
Der Zähler kann kleiner, gleich oder auch größer als der Nenner sein, z. B.:
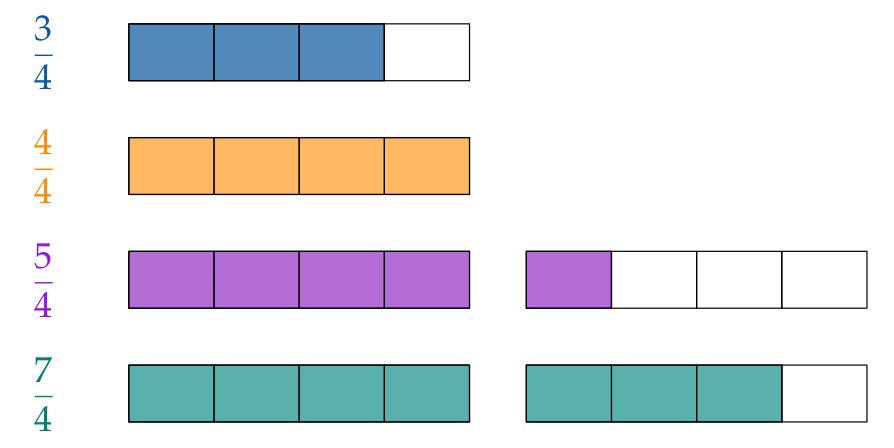
Solche Brüche bezeichnen mehr als ein Ganzes.
Den Anteil von etwas berechnen
Eine Wasserkaraffe füllen
In diese Karaffe passt ein Liter Wasser. Du musst sie nicht ganz füllen. Experimentiere mit der Wassermenge. Du kannst ablesen welcher Bruchteil sich dann in der Karaffe befindet.
Strecken zerteilen
Eine Strecke von $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\textrm{m}$ Länge erhält man, indem man …
- eine $1\,\text{m}$ lange Strecke in vier gleich lange Teile zerlegt und dann ...
- drei Teile davon nimmt:
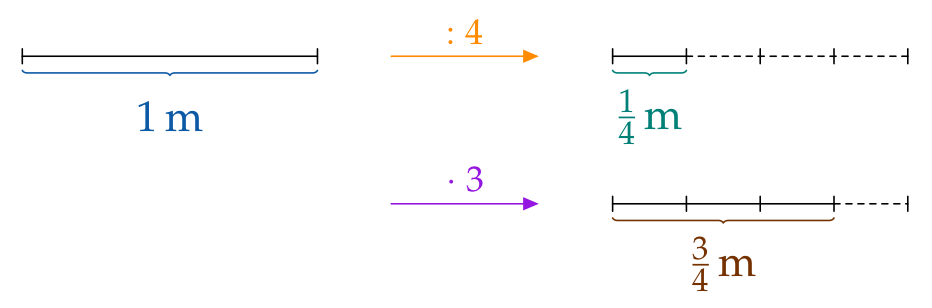
$\frac34\,\text{m}$ sind 3 Viertel von einem (ganzen) Meter.
Und ohne Skizze ...?
Löse die nächste Aufgabe ohne Hilfszeichnung.
So bestimmt man den Bruchteil eines Ganzen ganz einfach:
$$\frac{{\color{#9516E0}5}}{{\color{#FF8C00}7}}\text{ von }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#FF8C00}\,:\,}{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$Weißt du nicht weiter?
In manchen Aufgaben kannst du Tipps bekommen. Berühre dazu einfach die „Ampel“ oben rechts im Aufgabenfenster.
Und umgekehrt ...?
Wenn $\frac13$ einer Schulstunde $15\,\text{min}$ dauert, wie lange ist dann eine ganze Schulstunde?
$$15\,\text{min}\cdot \color{#0C5AA6}{3} = 45\,\text{min}$$Brüche mit Zähler 1 (z. B. $\frac13, \frac12$ oder $\frac17$) heißen Stammbrüche.
Wie du gerade gesehen hast, lässt sich das ursprüngliche Ganze sehr einfach berechnen, wenn der Anteil ein Stammbruch ist.
Wir überlegen uns wieder mit einer Strecke, wie man vorgehen muss, wenn der Anteil kein Stammbruch ist.
Zurück zur ganzen Strecke
Geht man von einer Strecke von $\frac34\,\text{m}$Länge aus, so erhält man eine Länge von einem Meter, indem man …
- die Strecke zuerst in in drei gleich lange Teile zerlegt und dann …
- vier solcher Teile aneinander legt:
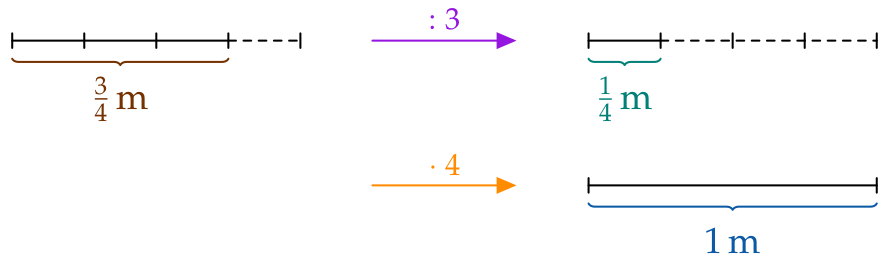
$\frac34\,\text{m}$ sind 3 Viertel von einem (ganzen) Meter.
Sind Anteil „$\frac{\color{#9516E0}5}{\color{#FF8C00}7}$“ und Bruchteil „$15\,\text{m}$“ gegeben, lässt sich wieder das Ganze bestimmen. Im Prinzip geht das „rückwärts“:
$$\Big({{15\,\text{m}}}~{\color{#9516E0}{:5}}\Big){\color{#FF8C00}\cdot}{\color{#FF8C00}7}= 3\,\text{m}{\color{#FF8C00}\cdot}{\color{#FF8C00}7}= {{21\,\text{m}}}$$
Pizza und Schokolade verteilen
Pizzabäcker Donatello hat Probleme in der Küche
Zu allem Überfluss wollen seine vier Gäste ihre Pizzen auch noch teilen.
Zusammenfassung
Da die die Pizzen gerecht verteilt werden sollen, bekommt jeder Gast immer gleich viel.
Am Ende hat jeder der Gäste jeweils $\frac14$ von drei Pizzen. Das ist genauso viel wie $\frac34$ von einer Pizza.
Drei Schokoriegel werden an vier Kinder verteilt
Tim, Karl, Willi und Gabi freuen sich sehr auf die drei Schokoriegel.
Strecken anders zerteilen
Den Bruchteil $\frac{\color{#9516E0}{3}}{\color{#FF8C00}{4}}\,\text{m}$ kann man auch so erhalten:
- Teile eine $3\,\text{m}$ lange Strecke in 4 gleich lange Teile und …
- nimm 1 Teil davon.
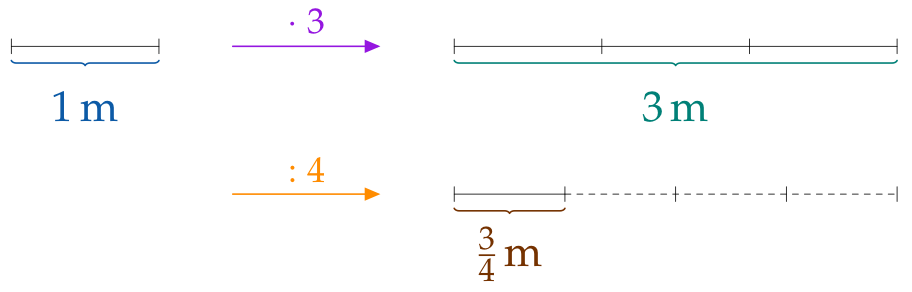
$\frac34\,\text{m}$ ist auch $\frac14$ von drei (ganzen) Metern.
Und ohne Skizze ...?
Löse die nächste Aufgabe ohne Hilfszeichnung.
Man kann den Bruchteil $\frac{\color{#9516E0}5}{\color{#FF8C00}7}$ von $21\,\text{m}$ auf zwei verschiedene Arten berechnen:
$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ von }{{21\,\text{m}}}= \Big({21\,\text{m}}{\color{#9516E0}\cdot}{\color{#9516E0}5}\Big)~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= 105\,{\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}= {15\,{\text{m}}}$$oder
$$\frac{\color{#9516E0}{5}}{\color{#FF8C00}{7}}\text{ von }{{21\,\text{m}}}= \Big({21\,\text{m}}~{\color{#FF8C00}:}\,{\color{#FF8C00}7}\Big){\color{#9516E0}\cdot}{\color{#9516E0}5}= 3\,\text{m}{\color{#9516E0}\cdot}{\color{#9516E0}5}= {15\,\text{m}}$$Beide Rechenwege sind richtig. Man bekommt das selbe Ergebnis.
Pauls Mathehausaufgabe
Paul ist in der vierten Klasse, sein Bruder Max schon in der sechsten. Paul löst seine Hausaufgaben und gibt sie Max zur Kontrolle:
Beliebige Zahlen teilen
Divisionsaufgaben, bei denen der Divisor größer ist als der Dividend, hast du bisher nicht lösen können. Du hast dafür die Schreibweise mit Rest genutzt:
$$\begin{aligned}3:11 &= 0\ \text{R}\ 3\\ 5:6& = 0\ \text{R}\ 5\end{aligned}$$Mit den Brüchen kommen wir jetzt ohne die Rest-Schreibweise aus. Die Rechnung ${\color{#0C5AA6}3}:\color{#FF8C00}{11}$ bedeutet:
„Teile 3 Ganze in 11 gleich große Stücke.“
Das Ergebnis ist der Bruch $\frac{\color{#0C5AA6}{3}}{\color{#FF8C00}{11}}$. Also: $$\begin{aligned}3:11 &= \frac{3}{11}\\[1em] 5:6& = \frac56\end{aligned}$$
Du kannst jede natürliche Zahl durch eine andere teilen, egal ob die Division aufgeht. Das Ergebnis schreibst du als Bruch.
Der Bruch $\frac{{\color{#0C5AA6}3}}{{\color{#FF8C00}4}}$ ist eine andere Schreibweise für den Quotienten ${\color{#0C5AA6}3}:{\color{#FF8C00}4}$
Mit Hilfe von Brüchen kann man alle natürlichen Zahlen durcheinander teilen, z. B.:
$3:4=\frac34,\quad 5:2=\frac52,\quad 3:7=\frac37,\quad 5:6=\frac56$
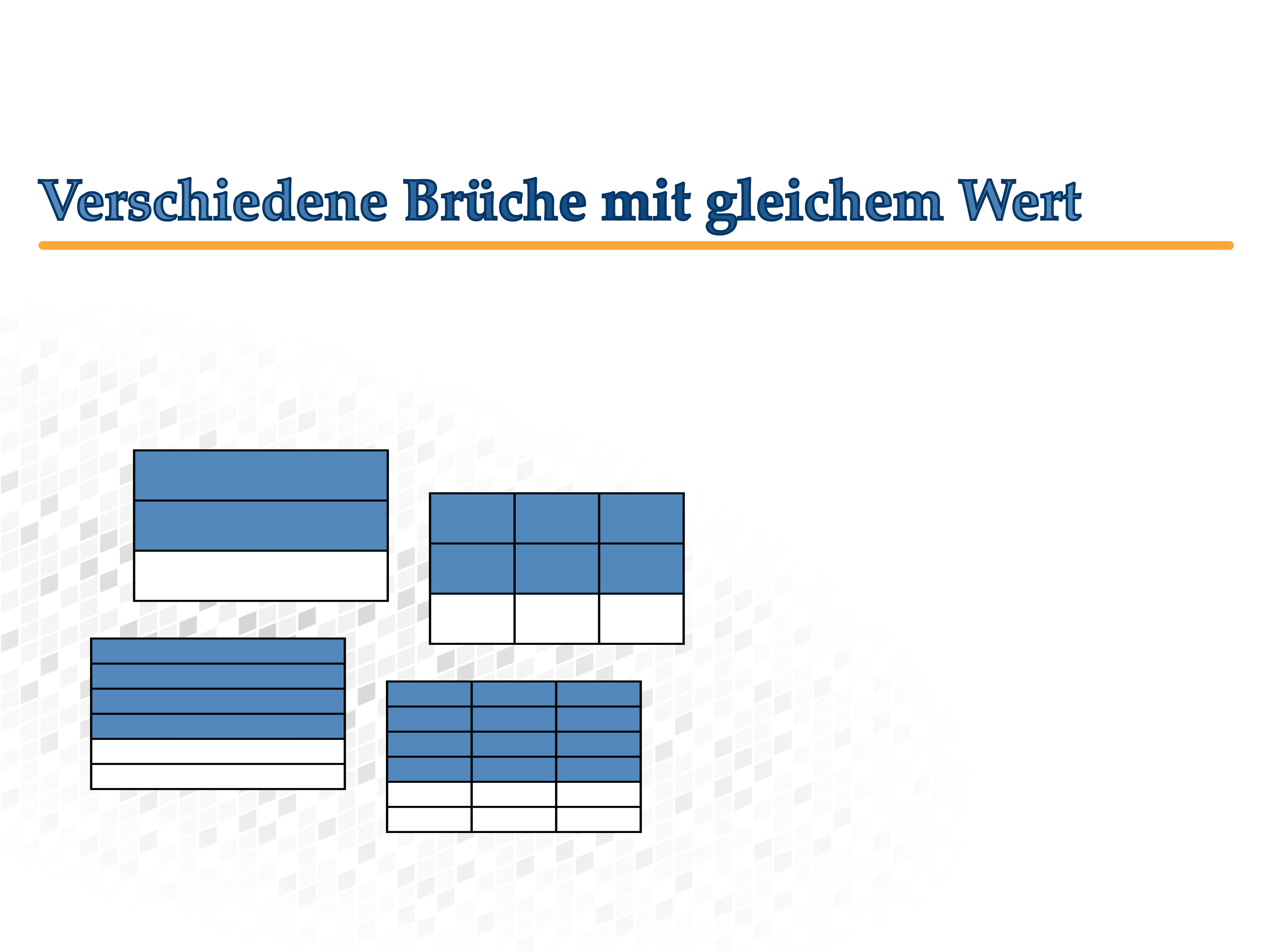
Verschiedene Brüche mit gleichem Wert
Ein Papier wird gefaltet
Schneide aus einem Blatt Papier ein Quadrat aus. Markiere dann die Hälfte des Quadrates farbig.
Verschiedene Brüche bezeichnen den selben Anteil
Finde mit Hilfe des Widgets verschiedene Brüche, die den selben Anteil des Kreises beschreiben.
Und jetzt ohne Bild …
Marie behauptet: „Ich habe gemerkt, dass ich einfach oben und unten immer das Selbe machen muss.“
Was meint Marie damit?
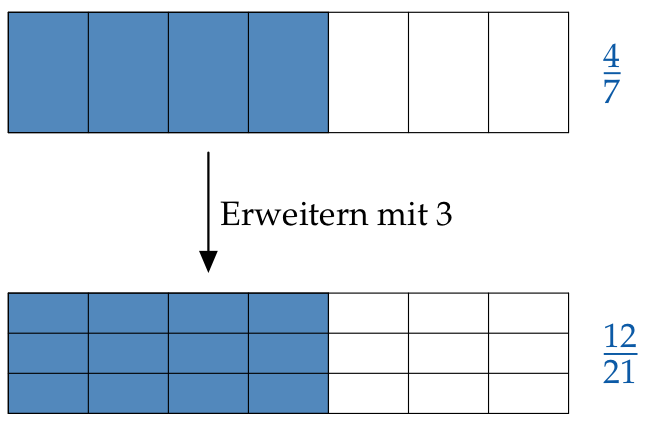
Erweitern heißt: Zähler und Nenner mit der selben Zahl multiplizieren.
Wir schreiben die Zahl, mit der wir den Bruch erweitern, über das Gleichheitszeichen:
$$\frac47 \begin{matrix} \color{#0C5AA6}3\\ =\\ \phantom{3} \end{matrix} \frac{4{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}{7{\color{#0C5AA6}\cdot}{\color{#0C5AA6}3}}=\frac{12}{21} $$Beim Erweitern wird die Einteilung feiner:
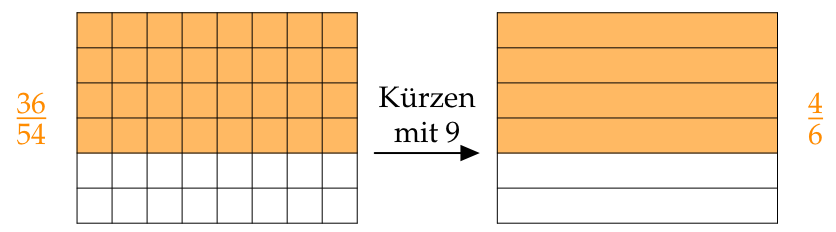
Kürzen heißt: Zähler und Nenner durch die selbe Zahl dividieren.
Wir notieren die Zahl, mit der wir den Bruch kürzen, unter das Gleichheitszeichen:
$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#FF8C00}8 \end{matrix} \frac{32{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}{48{\,\color{#FF8C00}:\,}{\color{#FF8C00}8}}= \frac{4}{6} $$Beim Kürzen wird die Einteilung gröber:
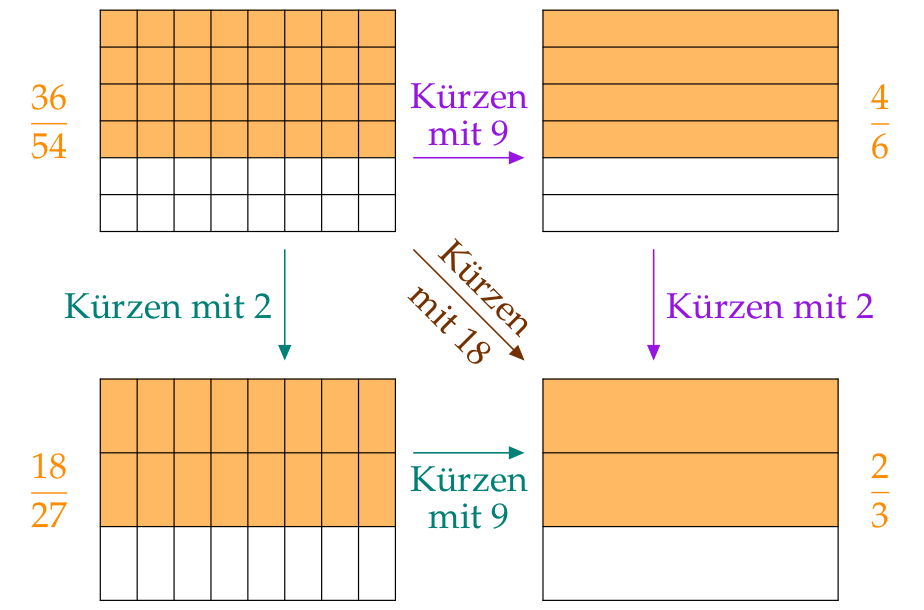
Immer weiter kürzen
Du kannst Brüche mit gemeinsamen Teilern von Zähler und Nenner kürzen.
Im Bruch $\frac{32}{48}$ haben der Zähler „32“ und der Nenner „48“ die gemeinsamen Teiler 8, 2 und 18. Wir können $\frac{32}{48}$ also auf verschiedene Arte kürzen:
Und jetzt ohne Bild …
Das können wir auch als Rechnung notieren:
$$ \frac{32}{48} \begin{matrix} \phantom{8}\\ =\\ \color{#9516E0}8 \end{matrix} \frac{32{\,\color{#9516E0}:\,}{\color{#9516E0}8}}{48{\,\color{#9516E0}:\,}{\color{#9516E0}8}}= \frac{4}{6} \begin{matrix} \phantom{2}\\ =\\ \color{#9516E0}2 \end{matrix} \frac{4{\,\color{#9516E0}:\,}{\color{#9516E0}2}}{6{\,\color{#9516E0}:\,}{\color{#9516E0}2}}= \frac23 $$oder
$$ \frac{32}{48} \begin{matrix} \phantom{2}\\ =\\ \color{#008077}2 \end{matrix} \frac{32{\,\color{#008077}:\,}{\color{#008077}2}}{48{\,\color{#008077}:\,}{\color{#008077}2}}= \frac{16}{24} \begin{matrix} \phantom{8}\\ =\\ \color{#008077}8 \end{matrix} \frac{16{\,\color{#008077}:\,}{\color{#008077}8}}{24{\,\color{#008077}:\,}{\color{#008077}8}}= \frac23 $$oder
$$ \frac{32}{48} \begin{matrix} \phantom{16}\\ =\\ \color{#753200}{16} \end{matrix} \frac{32{\,\color{#753200}:\,}{\color{#753200}{16}}}{48{\,\color{#753200}:\,}{\color{#753200}{16}}}= \frac23 $$Im Bruch $\frac23$ haben Zähler und Nenner keine gemeinsamen Teiler mehr. Einen solchen Bruch nennen wir vollständig gekürzt.
Erweitern und Kürzen ändert den Wert eines Bruches nicht.
Ein Bruch kann nur durch gemeinsame Teiler von Zähler und Nenner gekürzt werden.
Haben Zähler und Nenner eines Bruches keine gemeinsamen Teiler, nennt man den Bruch vollständig gekürzt.
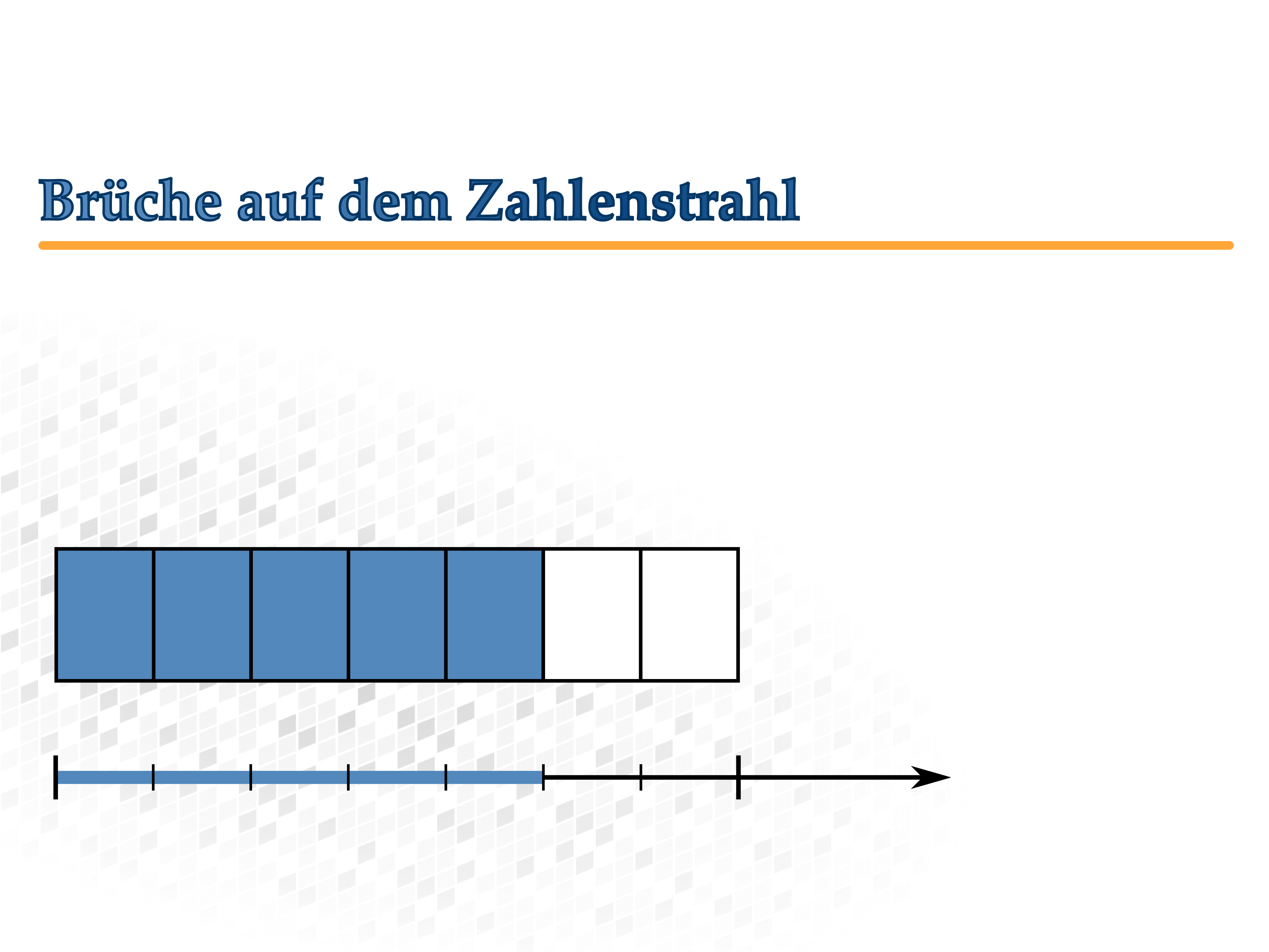
Brüche auf dem Zahlenstrahl
Einen Kreis abwickeln
Was bedeuten Brüche auf dem Zahlenstrahl?
Ein Rechteck schrumpfen
Du kannst dir den Zahlenstrahl auch als „geschrumpftes Rechteck“ vorstellen.
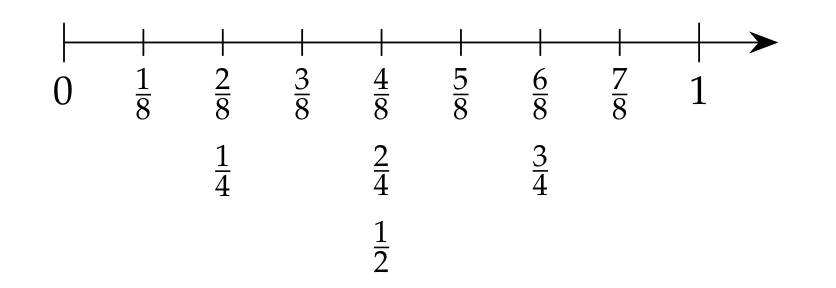
Brüche können auf dem Zahlenstrahl dargestellt werden. Dabei kann man sich den Zahlenstrahl als abgewickelten Kreis vorstellen:
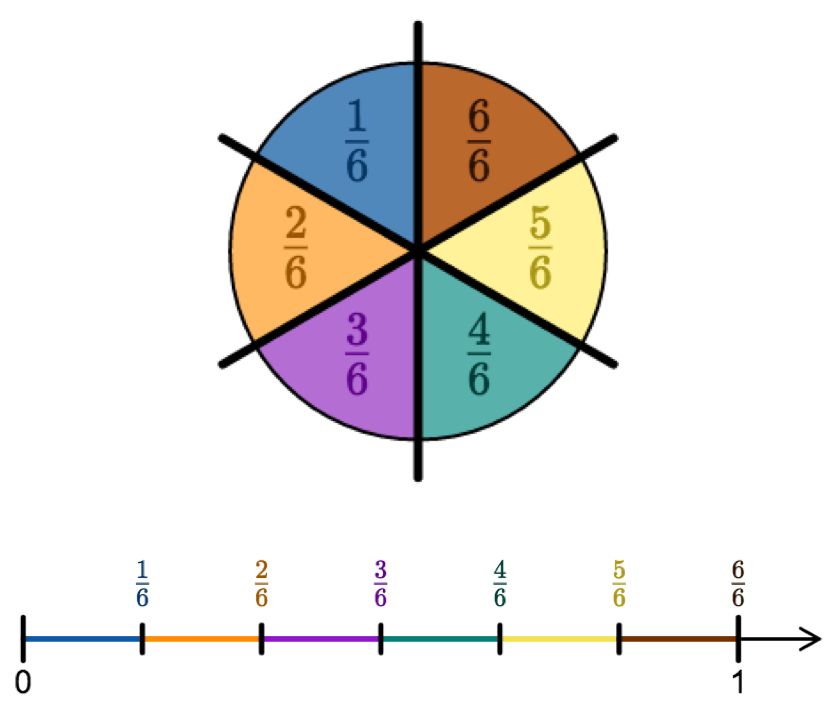
Brüche, die weniger als ein Ganzes sind, heißen echte Brüche. Sie liegen auf dem Zahlenstrahl zwischen der 0 und der 1. Ihr Zähler ist kleiner als ihr Nenner.
Und rechts von der 1?
Rechts von der 1 ist auf dem Zahlenstrahl noch endlos Platz. Hier liegen Brüche, die mehr sind als ein Ganzes.
Brüche können auch mehr als ein Ganzes beschreiben. Auf dem Zahlenstrahl sieht das so aus:
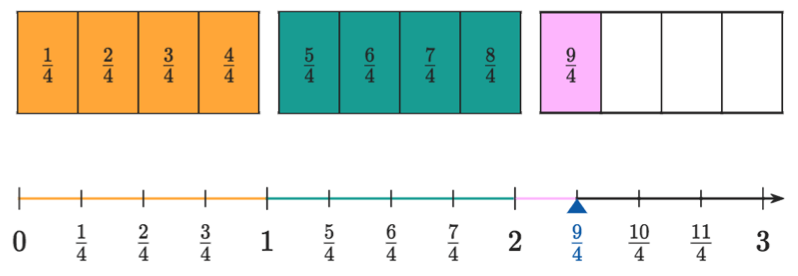
Brüche, die mehr als ein Ganzes beschreiben, heißen unechte Brüche. Sie liegen auf dem Zahlenstrahl rechts von der 1. Ihr Zähler ist größer als ihr Nenner.
Und zwischen den Einteilungen?
Manchmal reicht die Einteilung auf dem Zahlenstrahl nicht aus, um Brüche mit größerem Nenner eintragen zu können. Hier musst du die Einteilung verfeinern.
Wenn die Einteilung auf dem Zahlenstrahl nicht ausreicht, muss sie verfeinert werden:
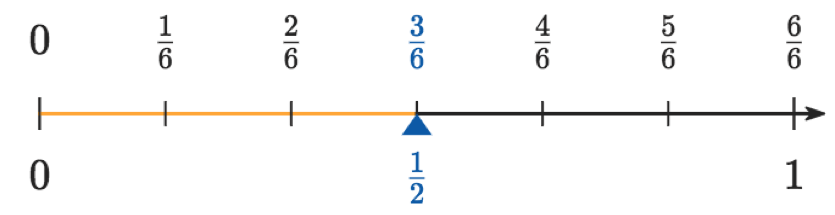
Platz schon besetzt?!
Manche Brüche teilen sich ihren Platz auf dem Zahlenstrahl:
In der Aufgabe hast du gesehen, dass die Brüche $\frac13$ und $\frac26$ an der selben Stelle auf dem Zahlenstrahl stehen. Bei den Brüchen $\frac{10}{6}$ und $\frac53$ war das auch der Fall.
Wenn du an das letzte Kapitel denkst, fällt dir schnell auf, warum diese Brüche den selben Platz belegen:
$$ \frac13 \begin{matrix} 2\\ =\\ \phantom{2} \end{matrix} \frac26 \quad \text{ und } \quad \frac{10}6 \begin{matrix} \phantom{2}\\ =\\ 2 \end{matrix} \frac{5}{3} $$Die Brüche haben den gleichen Wert, weil sie durch Erweitern und Kürzen ineinander umgewandelt werden können.
Zu jedem Bruch gehört ein Punkt auf der Zahlengeraden. Zu wertgleichen Brüchen gehört derselbe Punkt!
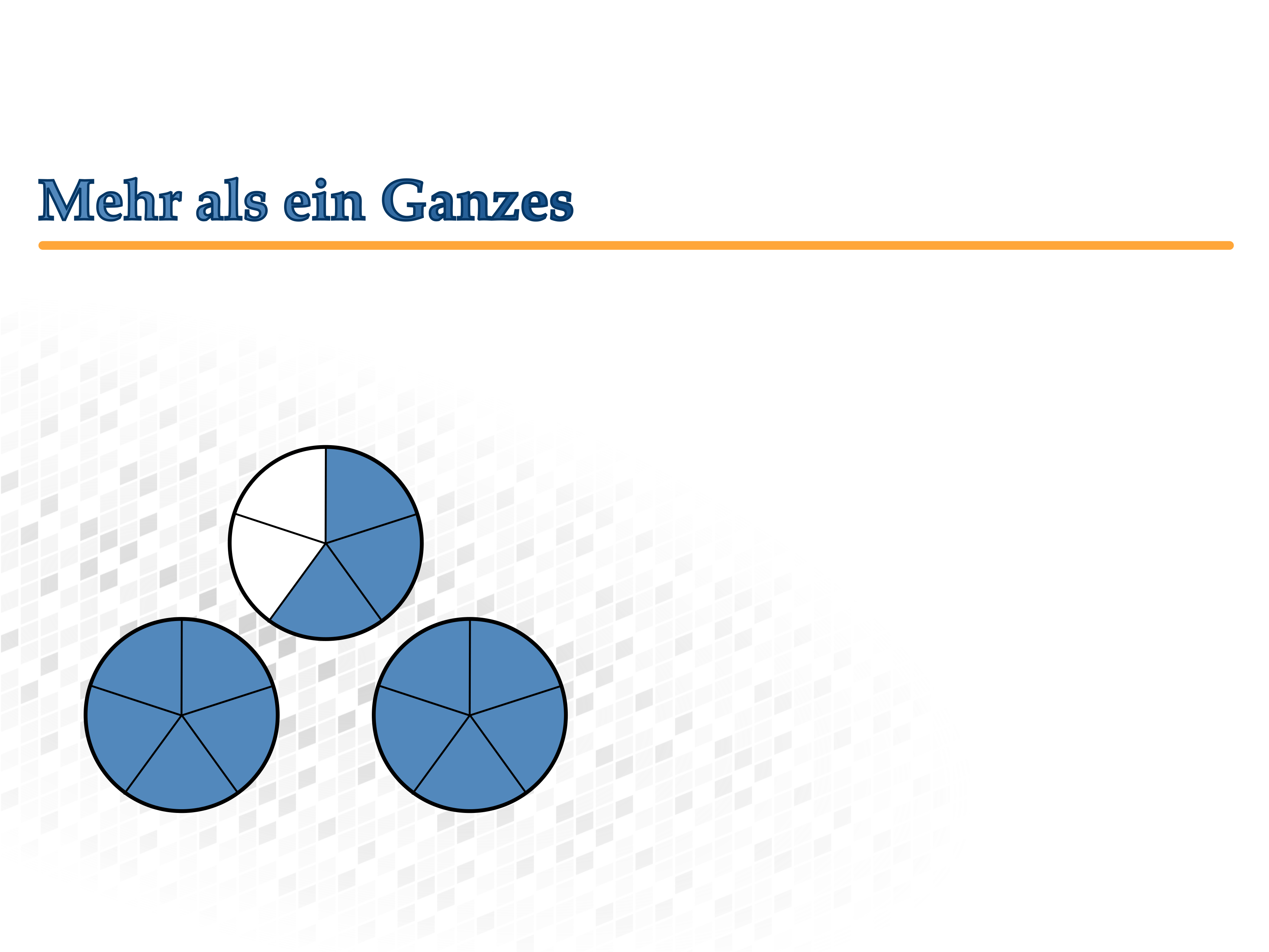
Mehr als ein Ganzes
Seltsame Brüche
Der Bruch $\frac{11}{3}$ ist ein unechter Bruch. Er liegt auf dem Zahlenstrahl rechts von der 1.
Oft ist es hilfreich zu wissen, wie viele Ganze in einem unechten Bruch stecken. Hierfür gibt es eine besondere Schreibweise, die gemischten Zahlen.
Gemischte Zahlen
Eine gemischte Zahl besteht aus zwei Teilen:
- Einer natürlichen Zahl, die angibt, wie viele Ganze im unechten Bruch stecken und ...
- einem echten Bruch, der den Rest angibt.
Bei $\frac{11}{3}$ sieht das so aus:
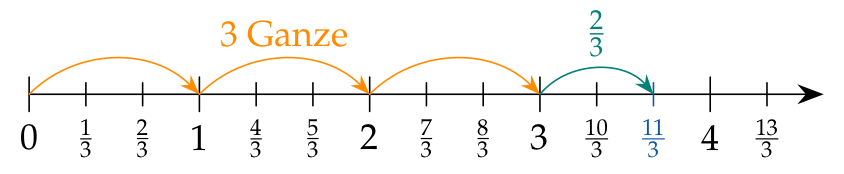
In der gemischten Schreibweise können wir unechte Brüche viel kürzer schreiben:
$$\frac{11}{3}= {\color{#FF8C00}{3\text{ Ganze}}} + {\color{#008077}{\frac{2}{3}}}= {\color{#0C5AA6}{3\,\frac{2}{3}}}$$Und ohne Zahlenstrahl …?
Hier siehst du eine andere Möglichkeit, den unechten Bruch $\frac{11}{3}$ in die gemischte Zahl $3\,\frac23$ umzuwandeln:
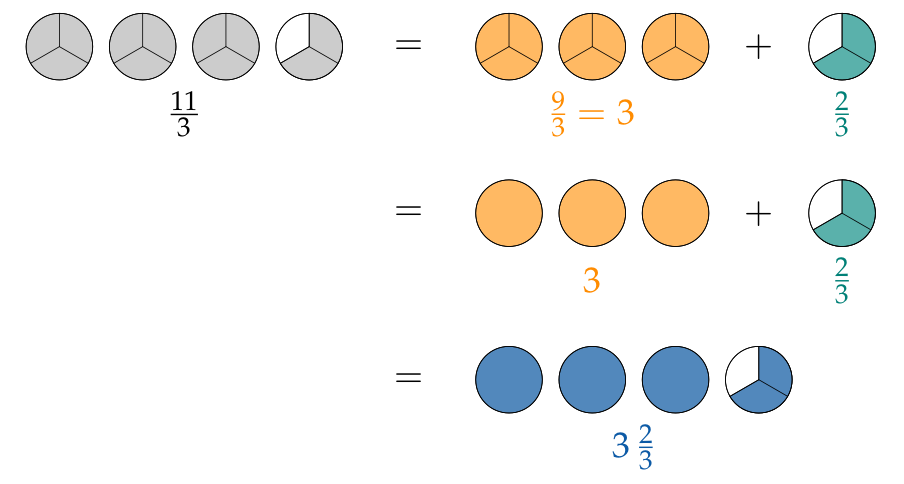
Unechte Brüche kann man als gemischte Zahlen schreiben:
$$\begin{aligned} \frac{11}{3}&= 11:3= {\color{#FF8C00}3}\text{ R }{\color{#008077}2}\\[1em] \frac{11}{3}&= 11:3= {\color{#FF8C00}3} +{\color{#008077}{\frac23}}= {\color{#0C5AA6}{3\,\frac23}}\end{aligned}$$Mit ein wenig Übung schaffst du den Umformungsschritt im Kopf! Du musst die Rechenschritte nicht aufschreiben.
Und anders herum … ?
Wir können auch anders herum aus einer gemischten Zahl wieder einen unechten Bruch machen:
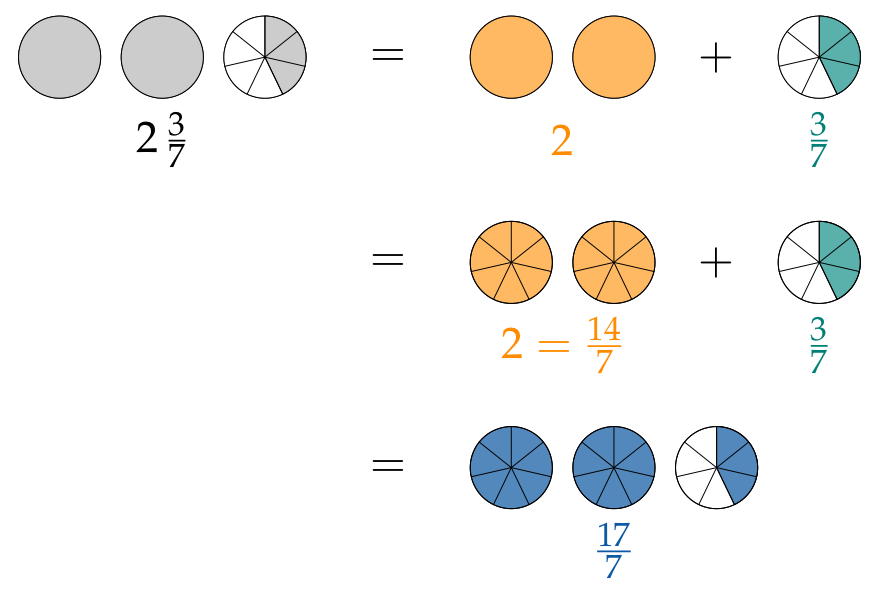
Gemischte Zahlen kann man auch wieder als unechte Brüche schreiben:
$$2\,\frac{3}{7}= {\color{#FF8C00}2} +{\color{#008077}{\frac{3}{7}}}= {\color{#FF8C00}{\frac{14}{7}}} +{\color{#008077}{\frac{3}{7}}}= {\color{#0C5AA6}{\frac{17}{7}}}$$Brüche, bei denen der Zähler größer ist als der Nenner, beschreiben mehr als ein Ganzes. Sie heißen unechte Brüche.
Wenn wir sie als gemischte Zahlen schreiben, wissen wir sofort, wo sie auf dem Zahlenstrahl liegen:
$$\frac{10}{3}= 3+\frac13= {\color{#0C5AA6}{3\,\frac13}}$$Er liegt auf dem Zahlenstrahl also zwischen 3 und 4.
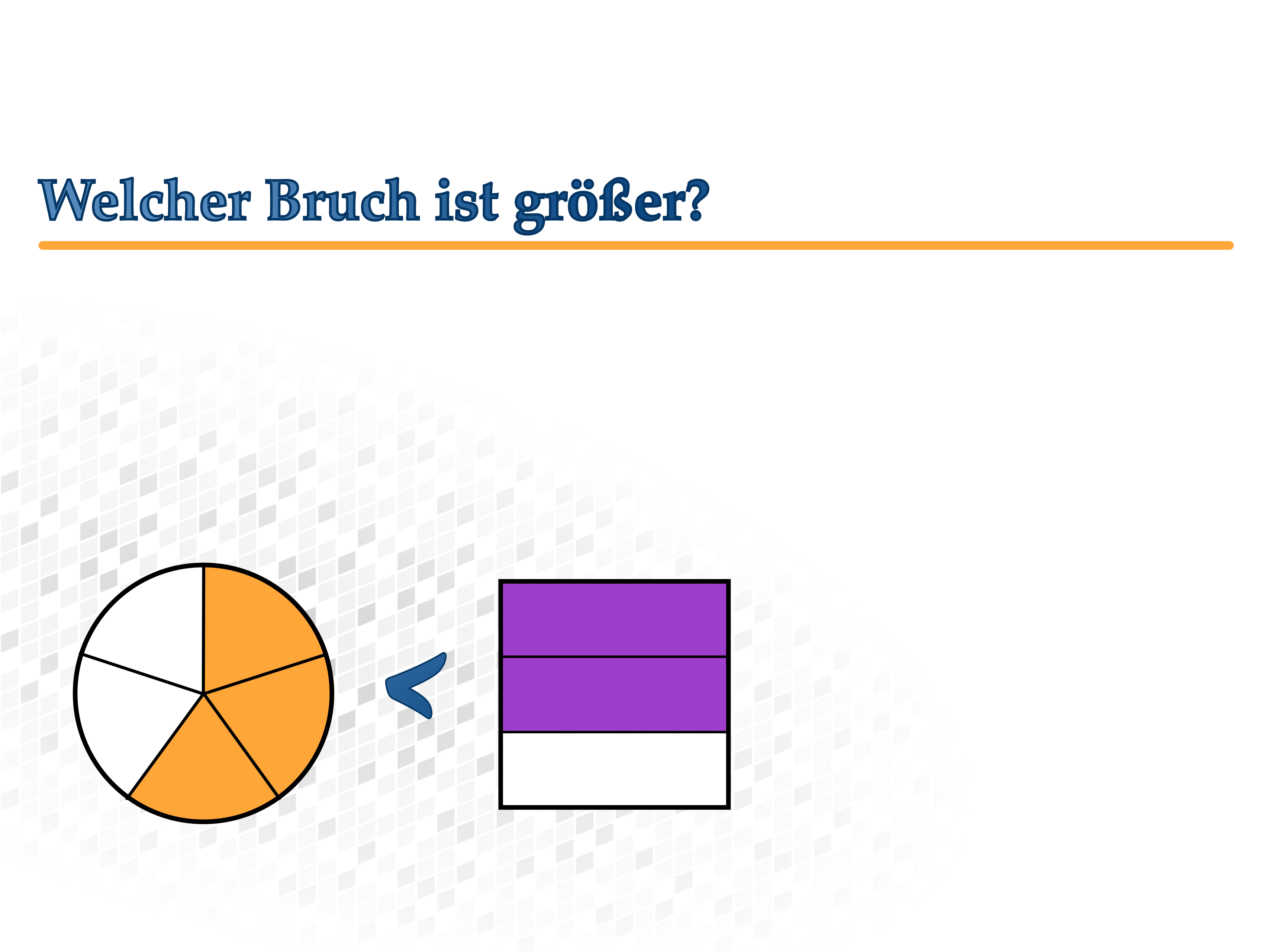
Welcher Bruch ist größer?
Weniger oder mehr als ein Ganzes?
Ob ein Bruch weniger oder mehr als ein Ganzes ist, kann man leicht entscheiden: Liegt er auf dem Zahlenstrahl links oder rechts von der 1?
Zur Erinnerung
Unechte Brüche sind Brüche, die mehr sind als ein Ganzes (z. B. $\frac54$ oder $\frac97$).
Echte Brüche sind Brüche, die weniger sind als ein Ganzes, (z. B. $\frac34$ oder $\frac78$).
Unechte Brüche (z. B. $\frac65$) sind mehr als ein Ganzes.
Sie sind immer größer als echte Brüche(z. B. $\frac78$ )
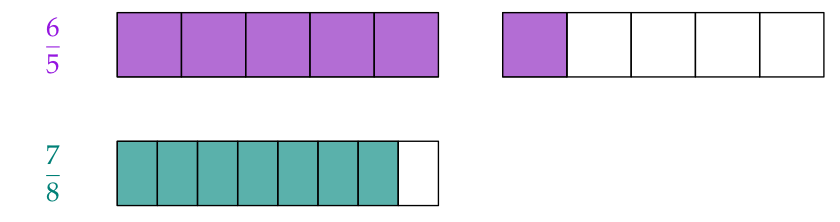$$\text{Also ist } {\color{#9516E0}{\frac{6}{5}}}>{\color{#008077}{\frac{7}{8}}}.$$
Nutze die Strategie, um die Aufgabe zu lösen:
Mehr oder weniger als die Hälfte?
Ob ein Bruch mehr oder weniger als die Hälfte vom Ganzen bezeichnet, lässt sich leicht herausfinden.Ist ein Bruch mehr als die Hälfte (z. B. $\frac47$) und ein anderer Bruch weniger als die Hälfte (z. B. $\frac35$), lassen sie sich leicht vergleichen:
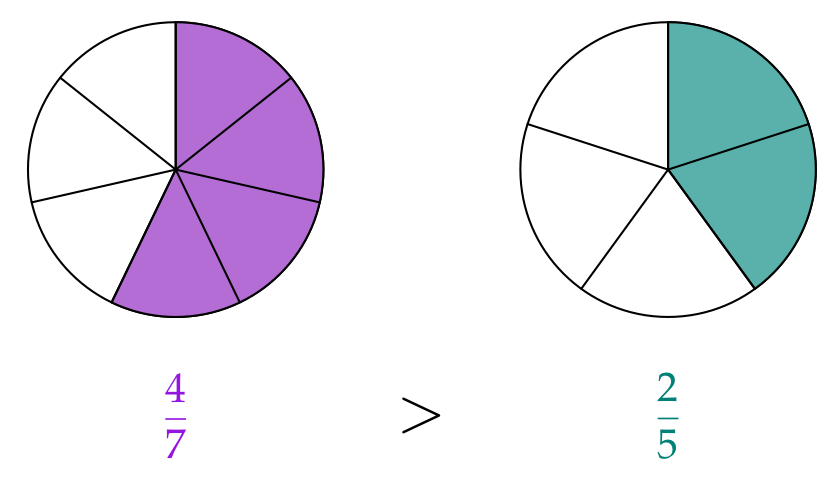
Nutze die Strategie, um die Aufgabe zu lösen:
Brüche mit Zähler 1
Für die nächsten Aufgaben brauchst du eine neue Strategie:
„Je kleiner der Nenner, desto größer die Stücke!“
Übrigens
Brüche mit Zähler 1 nennt man Stammbrüche.
Brüche mit gleichem Zähler
Bei Brüchen mit gleichem Zähler ist derjenige größer, der den kleineren Nenner hat.
Also der Bruch, bei dem das Ganze in weniger Stücke aufgeteilt ist:
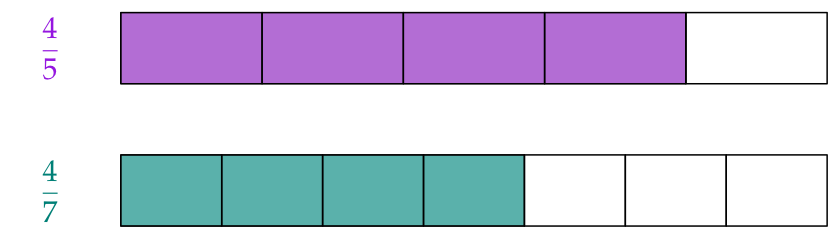$$\text{Also ist }{\color{#9516E0}{\frac{4}{5}}}>{\color{#008077}{\frac{4}{7}}}.$$
Brüche mit gleichem Nenner
Wenn der Nenner gleich ist, musst du nur herausfinden, welcher Bruch mehr Stücke beschreibt:
„Je kleiner der Zähler, desto weniger Stücke!“
Brüche mit gleichem Nenner heißen gleichnamige Brüche.
Bei gleichnamigen Brüchen ist der Bruch größer, der den größeren Zähler hat.
Also der Bruch, der mehr von den gleich großen Stücken hat:
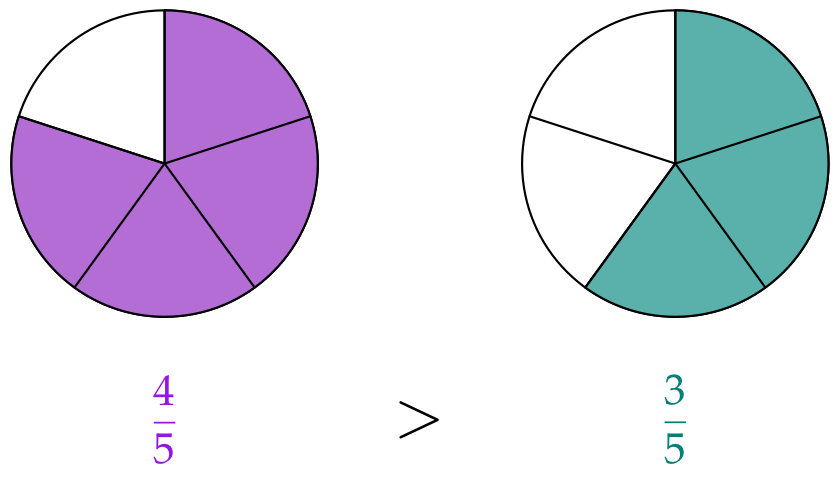
Achte in der nächsten Aufgabe darauf, ob die Brüche den gleichen Zähler oder den gleichen Nenner haben.
Schokolade genascht
Steffen und Franziska kaufen sich in der Mittagspause jeder eine Tafel Schokolade. Steffen hat $\frac14$ und Franziska $\frac{9}{32}$ der Tafel übrig.
Auf gleicher Zähler oder gleichen Nenner bringen?
Um zwei Brüche zu vergleichen, kannst du sie auf den gleichen Zähler oder den gleichen Nenner bringen. Meistens ist eine Variante einfacher:
Beispiel 1
Welcher Bruch ist größer, $\displaystyle\frac{2}{15}$ oder $\displaystyle\frac{3}{17}$?
| Mit gleichem Zähler: | $\displaystyle\color{#9516E0}{\frac{6}{45}}<\color{#008077}{\frac{6}{34}}$ |  |
| Mit gleichem Nenner: | $\displaystyle\color{#9516E0}{\frac{34}{255}}<\color{#008077}{\frac{45}{255}}$ |  |
Beispiel 2
Welcher Bruch ist größer, $\displaystyle\frac{13}{16}$ oder $\displaystyle\frac{3}{4}$?
| Mit gleichem Zähler: | $\displaystyle\color{#9516E0}{\frac{39}{48}}>\color{#008077}{\frac{39}{52}}$ | |
| Mit gleichem Nenner: | $\displaystyle\color{#9516E0}{\frac{13}{16}}>\color{#008077}{\frac{12}{16}}$ | |
Was geht einfacher?
Bringe die Brüche zum Vergleichen auf einen gemeinsamen Zähler oder Nenner. Entscheide selbst.